Mọi người giúp mình với.
Đề bài: Giải phương trình sau: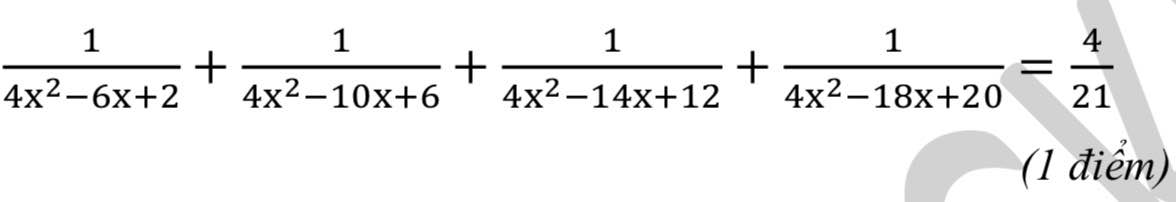
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
PP
1
Những câu hỏi liên quan
PP
1
8 tháng 12 2021
\(ĐK:x\ne\dfrac{1}{2};x\ne1;x\ne\dfrac{3}{2};x\ne2;x\ne\dfrac{5}{2}\\ PT\Leftrightarrow\dfrac{1}{\left(2x-1\right)\left(x-1\right)}+\dfrac{1}{\left(x-1\right)\left(3x-2\right)}+\dfrac{1}{\left(3x-2\right)\left(x-2\right)}+\dfrac{1}{\left(x-2\right)\left(5x-2\right)}=\dfrac{4}{21}\\ \Leftrightarrow2\left[\dfrac{\dfrac{1}{2}}{\left(x-\dfrac{1}{2}\right)\left(x-1\right)}+\dfrac{\dfrac{1}{2}}{\left(x-1\right)\left(x-\dfrac{3}{2}\right)}+\dfrac{\dfrac{1}{2}}{\left(x-\dfrac{3}{2}\right)\left(x-2\right)}+\dfrac{\dfrac{1}{2}}{\left(x-2\right)\left(x-\dfrac{5}{2}\right)}\right]=\dfrac{4}{21}\)
\(\Leftrightarrow\dfrac{1}{x-1}-\dfrac{1}{x-\dfrac{1}{2}}+\dfrac{1}{x-\dfrac{3}{2}}-\dfrac{1}{x-1}+\dfrac{1}{x-2}-\dfrac{1}{x-\dfrac{3}{2}}+\dfrac{1}{x-\dfrac{5}{2}}-\dfrac{1}{x-2}=\dfrac{2}{21}\\ \Leftrightarrow\dfrac{1}{x-1}-\dfrac{1}{x-\dfrac{5}{2}}=\dfrac{2}{21}\\ \Leftrightarrow\dfrac{x-\dfrac{5}{2}-x+1}{\left(x-1\right)\left(x-\dfrac{5}{2}\right)}=\dfrac{2}{21}\\ \Leftrightarrow\dfrac{-\dfrac{3}{2}}{x^2-\dfrac{7}{2}x+\dfrac{5}{2}}=\dfrac{2}{21}\\ \Leftrightarrow x^2-\dfrac{7}{2}x+\dfrac{5}{2}=-\dfrac{63}{4}\\ \Leftrightarrow4x^2-14x+10=-63\\ \Leftrightarrow4x^2-14x+73=0\\ \Leftrightarrow x\in\varnothing\)
14 tháng 2 2022
a. \(ZnCl_2+Zn^{2+}+2Cl^-\)
b. \(FeSO_4\rightarrow Fe^{2+}+SO_4^{2-}\)
c. \(Zn\left(NO_3\right)_2\rightarrow Zn^{2+}+2NO_3^-\)
d. \(MgCl_2\rightarrow Mg^{2+}+2Cl^-\)
KV
23 tháng 4 2021
\(\dfrac{x+2}{x-1}=\dfrac{x-1}{x-3}\) (1)
ĐKXĐ: \(x\ne1;x\ne3\)
(1) \(\Leftrightarrow\left(x+2\right)\left(x-3\right)=\left(x-1\right)^2\)
\(\Leftrightarrow x^2-3x+2x-6=x^2-2x+1\)
\(\Leftrightarrow-3x+2x+2x=1+6\)
\(\Leftrightarrow x=7\) (nhận)
Vậy S = {7}
20 tháng 2 2022
Bài 8:
a: Khi a=1 thì phương trình sẽ là \(\left(1-4\right)x-12x+7=0\)
=>-3x-12x+7=0
=>-15x+7=0
=>-15x=-7
hay x=7/15
b: Thay x=1 vào pt, ta được:
\(a^2-4-12+7=0\)
\(\Leftrightarrow\left(a-3\right)\left(a+3\right)=0\)
hay \(a\in\left\{3;-3\right\}\)
c: Pt suy ra là \(\left(a^2-16\right)x+7=0\)
Để phương trình đã cho luôn có một nghiệm duy nhất thì (a-4)(a+4)<>0
hay \(a\notin\left\{4;-4\right\}\)
10 tháng 1 2023
=>0,2x+0,4-0,5x=0,25-0,5x+0,25
=>0,2x+0,4=0,5
=>0,2x=0,1
=>x=1/2
2 tháng 7 2021
\(2sin^2\dfrac{x}{2}=cos5x+1\)
\(\Leftrightarrow-cos5x=1-2.sin^2\dfrac{x}{2}\)
\(\Leftrightarrow-cos5x=cosx\)
\(\Leftrightarrow cos\left(5x\right)=cos\left(\pi-x\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}5x=\pi-x+k2\pi\\5x=-\pi+x+k2\pi\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+\dfrac{k\pi}{3}\\x=-\dfrac{\pi}{4}+\dfrac{k\pi}{2}\end{matrix}\right.\) (k nguyên)
Vậy..
10 tháng 3 2020
<=> (x2 - 2x)2 + x2 - 2x + 1 - 13 = 0
<=> (x2 - 2x)2 + x2 - 2x - 12 = 0
Đặt t = x2 - 2x
Khi đó ta có pt: t2 + t - 12 = 0
<=> t2 + 4t - 3t - 12 = 0
<=> (t - 3)(t + 4) = 0 <=> \(\orbr{\begin{cases}t=3\\t=-4\end{cases}}\)
*Với t = 3 ta có: x2 - 2x = 3
<=> x2 - 2x - 3 = 0
<=> (x - 3)(x + 1) = 0 <=> \(\orbr{\begin{cases}x=3\\x=-1\end{cases}}\)
*Với t = -4 ta có: x2 - 2x = -4
<=> x2 - 2x + 4 = 0
<=> (x - 1)2 + 3 = 0 (Vô nghiệm)
Vậy S = {3;-1}
10 tháng 3 2020
(x2-2x)2 + (x-1)2 - 13 = 0
<=> x^4 - 4x^3 + 4x^2 + x^2 - 2x + 1 - 13 = 0
<=> x^3 - 4x^3 + 5x^2 - 2x - 12 = 0
<=> x^4 + x^3 - 5x^3 - 5x^2 + 10x^2 + 10x - 12x - 12 = 0
<=> x^3(x + 1) - 5x^2(x + 1) + 10x(x + 1) - 12(x + 1) = 0
<=> (x^3 - 5x^2 + 10x - 12)(x + 1) = 0
<=> (x^3 - 3x^2 - 2x^2 + 6x + 4x - 12)(x + 1) = 0
<=> [x^2(x - 3) - 2x(x - 3) + 4(x - 3)](x + 1) = 0
<=> (x^2 - 2x + 4)(x - 3)(x + 1) = 0
có x^2 - 2x + 4 = (x - 1)^2 + 3 lớn hơn 0
<=> x - 3 = 0 hoặc x + 1 = 0
<=> x = 3 hoặc x = -1
19 tháng 8 2021
Bài 1:
ĐKXĐ: \(x\ge\dfrac{1}{2}\)
Ta có: \(\sqrt{5x^2}=2x-1\)
\(\Leftrightarrow5x^2=\left(2x-1\right)^2\)
\(\Leftrightarrow5x^2-4x^2+4x-1=0\)
\(\Leftrightarrow x^2+4x-1=0\)
\(\text{Δ}=4^2-4\cdot1\cdot\left(-1\right)=20\)
Vì Δ>0 nên phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{-4-2\sqrt{5}}{2}=-2-\sqrt{5}\left(loại\right)\\x_2=\dfrac{-4+2\sqrt{5}}{2}=-2+\sqrt{5}\left(loại\right)\end{matrix}\right.\)
AH
Akai Haruma
Giáo viên
19 tháng 8 2021
Bài 1: Bình phương hai vế lên có giải ra được kết quả. Nhưng phải kèm thêm điều kiện $2x-1\geq 0$ do $\sqrt{5x^2}\geq 0$
PT \(\Leftrightarrow \left\{\begin{matrix} 2x-1\geq 0\\ 5x^2=(2x-1)^2\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ x^2+4x-1=0\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ (x+2)^2-5=0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ (x+2-\sqrt{5})(x+2+\sqrt{5})=0\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ x=-2\pm \sqrt{5}\end{matrix}\right.\) (vô lý)
Vậy pt vô nghiệm.
NV
0
\(\Rightarrow\dfrac{1}{\left(2x-1\right)\left(2x-2\right)}+\dfrac{1}{\left(2x-2\right)\left(2x-3\right)}+\dfrac{1}{\left(2x-3\right)\left(2x-4\right)}+\dfrac{1}{\left(2x-4\right)\left(2x-5\right)}=\dfrac{4}{21}\)
\(\Rightarrow\dfrac{1}{2x-2}-\dfrac{1}{2x-1}+\dfrac{1}{2x-3}-\dfrac{1}{2x-2}+\dfrac{1}{2x-4}-\dfrac{1}{2x-3}+\dfrac{1}{2x-5}-\dfrac{1}{2x-4}=\dfrac{4}{21}\)
\(\Rightarrow\dfrac{1}{2x-5}-\dfrac{1}{2x-1}=\dfrac{4}{21}\)
\(\Rightarrow\dfrac{4}{\left(2x-1\right)\left(2x-5\right)}=\dfrac{4}{21}\)
\(\Rightarrow\left(2x-1\right)\left(2x-5\right)=21\)
\(\Rightarrow4x^2-12x-16=0\Rightarrow\left[{}\begin{matrix}x=-1\\x=4\end{matrix}\right.\)