Cho tam giác MNP có \(\widehat{M}\) = 25o. \(\widehat{N}\) = 80o thì góc ngoài của tam giác tại đỉnh P có số đo bằng?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


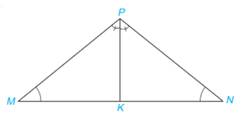
a)
Xét tam giác MPK có:
\(\widehat {PKM} + \widehat {MPK} + \widehat {KMP} = {180^o}\)
Xét tam giác NPK có:
\(\widehat {PKN} + \widehat {NPK} + \widehat {KNP} = {180^o}\)
Mà \(\widehat {KMP} = \widehat {KNP};\,\,\,\widehat {MPK} = \widehat {NPK}\)
Suy ra \(\widehat {MKP} = \widehat {NKP}\).
b)Xét hai tam giác MPK và NPK có:
\(\widehat {MPK} = \widehat {NPK}\)
PK chung
\(\widehat {MKP} = \widehat {NKP}\)
=>\(\Delta MPK = \Delta NPK\)(g.c.g)
c) Do \(\Delta MPK = \Delta NPK\) nên MP=NP (2 cạnh tương ứng)
=> Tam giác MNP cân tại P.

vvvv
Không spam nha. Chương trình game xin tặng chương trình học online. Nhằm mục đích game được nhiều người chơi.
Thay mặt người đào tạo chương trình hôm nay : Có 200 suất học bỗng cho những học sinh tích cực hoạt động từ bây giờ ( Mỗi suất học bỗng là 100k). Nhận thưởng bằng cách vào google tìm kiếm.
Link như sau vào google hoặc cốc cốc để tìm kiếm:
https://lazi.vn/quiz/d/17912/game-lien-quan-mobile-ra-doi-vao-ngay-thang-nam-nao
Copy cũng được nha
Bạn vào nick này hack nick mình thu ib dưới vs nha giúp mk chuyện này

Xét tam giác ABC có :
A + ABC + ACB = 180 *
=> ABC + ACB = 180* - a
Mà BC là phân giác ABC
=> ABD = CBD = \(\frac{1}{2}ABC\)
Mà CE là phân giác ACB
=> ACE = BCE = \(\frac{ACB}{2}\)
=> ECB + DBC = \(\frac{ACB+ABC}{2}\)= \(\frac{180-a}{2}\)
Xét tam giác OBC có :
OBC + OCB + BOC = 180*
=> BOC = 180* - ( OBC + OCB)
=> BOC = 180* - \(\frac{180-a}{2}\)
=> BOC =\(\frac{a}{2}\)(dpcm)

Ta có: 5\(\widehat{M}\) = 3\(\widehat{N}\) => \(\frac{\widehat{M}}{3}\) = \(\frac{\widehat{N}}{5}\) => \(\frac{7\widehat{M}}{21}\) = \(\frac{4\widehat{N}}{20}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{7\widehat{M}}{21}\) = \(\frac{4\widehat{N}}{20}\) = \(\frac{7\widehat{M}-4\widehat{N}}{21-20}\) = 15o
Do \(\frac{7\widehat{M}}{21}\) = 15 => \(\widehat{M}\) = 45
\(\frac{4\widehat{N}}{20}\) = 15 => \(\widehat{N}\) = 75
Áp dụng tính chất tổng 3 góc trong 1 tam giác ta có:
\(\widehat{M}\) + \(\widehat{N}\) + \(\widehat{P}\) = 180 độ
=> 45 + 75 + \(\widehat{P}\) = 180
=> \(\widehat{P}\) = 60o
Vậy \(\widehat{P}\) = 60o.
105 độ
1050