Từ mỗi hộp có 7 quả cầu trắng, 5 quả cầu đen lấy ngẫu nhiên đồng thời 4 quả . Tính sác xuất sao cho :
a/ bốn quả lấy ra cùng màu
b/ có ít nhất 1 quả cầu đen
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
19 tháng 11 2017
Không gian mẫu là kết quả việc chọn ngẫu nhiên 4 quả cầu từ hộp 10 quả cầu.
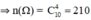
a. A: “ Bốn quả lấy ra cùng màu”
TH1: Bốn quả lấy ra cùng đen
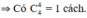
TH2: Bốn quả lấy ra cùng trắng
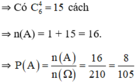
b. B: “ Cả 4 quả lấy ra đều màu đen”
⇒ B−: “ Có ít nhất 1 quả màu trắng”.
HP
15 tháng 12 2021
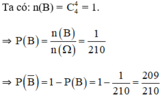
a, Gọi T là biến cố "Trong 4 quả lấy ra có 3 quả cầu trắng".
\(\left|\Omega\right|=C^4_{15}\)
\(\left|\Omega_T\right|=C^3_7.C^1_8\)
\(\Rightarrow P\left(T\right)=\dfrac{\left|\Omega_T\right|}{\left|\Omega\right|}=\dfrac{C^3_7.C^1_8}{C^4_{15}}=\dfrac{8}{39}\)
CM
19 tháng 7 2018
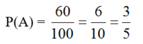
a) Không gian mẫu là kết quả của việc lấy ngẫu nhiên 1 quả cầu ở hộp thứ nhất và một quả cầu ở hộp thứ hai
+ Có 10 cách lấy 1 quả cầu bất kì ở hộp 1 và có 10 cách lấy 1 quả cầu bất kì ở hộp 2. Nên số phần tử của không gian mẫu là;
⇒ n(Ω) = 10.10 = 100.
A: “ Quả cầu lấy từ hộp thứ nhất trắng”
⇒ Có 6 cách lấy quả cầu màu trắng ở hộp A và 10 cách lấy quả cầu ở hộp B
⇒ n(A) = 6.10 = 60.
B: “Quả cầu lấy từ hộp thứ hai trắng”
⇒ Có 4 cách lấy quả cầu màu trắng ở hộp B và 10 cách lấy quả cầu ở hộp A
⇒ n(B) = 4.10 = 40.
A.B: “Cả hai quả cầu lấy ra đều trắng”
⇒ Có 6 cách lấy quả cầu màu trắng ở hộp A và 4 cách lấy quả cầu màu trắng ở hộp B
⇒ n(A.B) = 6.4 = 24.
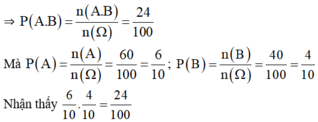
hay P(A.B) = P(A).P(B)
⇒ A và B là biến cố độc lập.
b) Gọi C: “Hai quả cầu lấy ra cùng màu”.
Ta có: A− : “Quả cầu lấy ra từ hộp thứ nhất màu đen”
B− : “ Quả cầu lấy ra từ hộp thứ hai màu đen”
⇒A−.B− : “Cả hai quả cầu lấy ra đều màu đen”
Nhận thấy A.B và A−.B− xung khắc (Vì không thể cùng lúc xảy ra hai trường hợp 2 quả cầu lấy ra cùng trắng và cùng đen)
Và C=(A.B)∪(A−.B−)
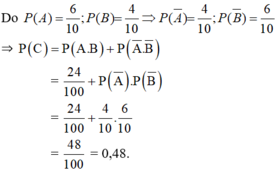
c) C− : “Hai quả cầu lấy ra khác màu”
⇒ P(C− )=1-P(C)=1-0,48=0,52
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 12 2022
Không gian mẫu: lấy 4 quả cầu từ 13 quả cầu có \(C_{13}^4\) cách
Lấy ra 4 quả cầu sao cho chỉ có màu trắng: \(C_6^4\) cách
Lấy ra 4 quả cầu sao cho chỉ có màu đen: \(C_7^4\) cách
\(\Rightarrow\) Số cách lấy ra 4 quả cầu có đủ 2 màu là: \(C_{13}^4-\left(C_6^4+C_7^4\right)\)
Xác suất: \(P=\dfrac{C_{13}^4-\left(C_6^4+C_7^4\right)}{C_{13}^4}=...\)
MH
9 tháng 4 2017
Phép thử T được xét là: "Từ mỗi hộp lấy ngẫu nhiên một quả cầu".
Mỗi một kết quả có thể có của phép thư T gồm hai thành phần là: 1 quả cầu của hộp thứ nhất và 1 quả cầu của hộp thứ 2.
Có 10 cách để lấy ra 1 quả cầu ở hộp thứ nhất và có 10 cách để lấy 1 quả cầu ở hộp thứ 2. Từ đó, vận dụng quy tắc nhân ta tìm được số các cách để lập được một kết quả có thể có của hai phép thử T là 10 . 10 = 100. Suy ra số các kết quả có thể có của phép thử T là n(Ω) = 100.
Vì lấy ngầu nhiên nên các kết quả có thể có của phép thử T là đồng khả năng.
Xét biến cố A: "Quả cầu lấy từ hộp thứ nhất có màu trắng".
Mỗi một kết quả có thể có thuận lợi cho A gồm 2 thành phần là: 1 quả cầu trắng ở hợp thứ nhất và 1 quả cầu (nào đó) ở hộp thứ 2. Vận dụng quy tắc nhân ta tìm được số các kết quả có thể có thuận lợi cho A là: n(A) = 6 . 10 = 60.
Suy ra P(A) = = 0,6.
Xét biến cố B: "Quả cầu lấy từ hộp thứ hai có màu trắng".
Tương tự như trên ta tìm được số các kết quả có thể thuận lợi cho B là:
n(B) = 10 . 4 = 40.
Từ đó suy ra P(B) = = 0,4.
a) Ta có A . B là biến cố: "Lấy được 1 cầu trắng ở hộp thứ nhất và 1 cầu trắng ở hộp thứ hai". Vận dụng quy tắc nhân ta tìm được số các kết quả có thể có thuận lợi cho A . B là:
6 . 4 =24. Suy ra:
P(A . B) = = 0,24 = 0,6 . 0,4 = P(A) . P(B).
Như vậy, ta có P(A . B) = P(A) . P(B). Suy ra A và B là hai biến cố độc lập với nhau.
b) Gọi C là biến cố: "Lấy được hai quả cầu cùng màu". Ta có
C = A . B + .
.
Trong đó = "Quả cầu lấy từ hộp thứ nhất có màu đen" và P(
) = 0,4.
: "Quả cầu lấy từ hộp thứ hai có màu đen" và P(
) = 0,6.
Và ta có A . B và .
là hai biến cố xung khắc với nhau.
A và B độc lập với nhau, nên và
cũng độc lập với nhau.
Qua trên suy ra;
P(C) = P(A . B + .
) = P(A . B) + P(
.
) = P(A) . P(B) + P(
) . P(
)
= 0,6 . 0,4 + 0,4 . 0,6 = 0,48.
c) Gọi D là biến cố: "Lấy được hai quả cầu khác màu". Ta có
D = => P(D) = 1 - P(C) = 1 - 0,48 = 0,52.
a, Gọi A là biến cố "Lấy ra bốn quả cùng màu".
\(\Rightarrow\left|\Omega\right|=C^4_{12}\)
\(\left|\Omega_A\right|=C^4_7+C^4_5\)
\(\Rightarrow P\left(A\right)=\dfrac{\left|\Omega_A\right|}{\left|\Omega\right|}=\dfrac{C^4_7+C^4_5}{C^4_{12}}=\dfrac{8}{99}\)
b, Gọi B là biến cố "Lấy ra một quả màu đen".
\(\Rightarrow\overline{B}\) là biến cố "Không lấy ra quả màu đen nào".
\(\Rightarrow\left|\Omega\right|=C^4_{12}\)
\(\left|\Omega_{\overline{B}}\right|=C^4_7\)
\(\Rightarrow P\left(\overline{B}\right)=\dfrac{C^4_7}{C^4_{12}}=\dfrac{7}{99}\)
\(\Rightarrow P\left(B\right)=1-P\left(\overline{B}\right)=\dfrac{92}{99}\)