x4 +5x =120
x=............
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
21 tháng 3 2018
Xét u = x 4 - 38 x 2 + 120 x + 4 m trên đoạn [0;2] ta có
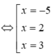
Vậy
Khi đó
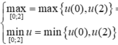
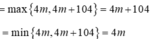
⇔ - 26 ≤ m ≤ 0
Có 27 số nguyên thoả mãn.
Chọn đáp án D.
CM
23 tháng 3 2019
Chọn D
Xét 
trên đoạn [0;2], ta có:
Vậy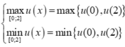 
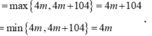
Cách 1:
Nếu 4m > 0 thì 
Nếu 4m + 104 < 0
⇔
m < -126 thì 
Nếu 
thì 
Vậy có 27 số nguyên thỏa mãn.
Cách 2:
Khi đó 
Có 27 số nguyên thoả mãn.
CM
24 tháng 5 2017
Chọn đáp án D.
Xét y = x 4 - 38 x 2 + 120 x + 4 m trên đoạn 0 ; 2 ta có
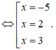
Vậy
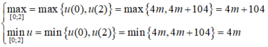
Có 27 số nguyên thoả mãn.
CM
22 tháng 3 2018
Chọn B
Xét f(x) = x 4 - 38 x 2 + 120 x + 4 m trên đoạn [0;2] ta có:
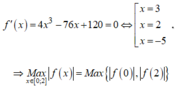
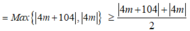
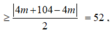
Dấu “=” xảy ra khi và chỉ khi 
Nhận xét: Với trắc nghiệm thì ta thử đáp án được đáp án B
9 tháng 3 2020
5x2-120x-125=0
x(5x-120)=0+125
x(5x-120)=125
\(\Rightarrow\orbr{\begin{cases}x=125\\5x-120=125\Rightarrow5x=125-120\Rightarrow5x=5\Rightarrow x=5:5=1\end{cases}}\)
Vậy x=125 hoặc x=1
9 tháng 3 2020
\(5x^2-120x-125=0\)
\(5\left(x^2-24x-25\right)=0\)
\(5\left(x-25\right)\left(x+1\right)=0\)
\(\Rightarrow5=0\)vô nghiệm
\(\Rightarrow\orbr{\begin{cases}x-25=0\\x+1=0\end{cases}\Rightarrow\orbr{\begin{cases}x=25\\x=-1\end{cases}}}\)
21 tháng 1 2024
\(\dfrac{20x^2+120x+180}{\left(3x+5\right)^2-4x^2}+\dfrac{5x^2-25}{9x^2-\left(2x+5\right)^2}-\dfrac{\left(2x+3\right)^2-x^2}{3\left(x^2+8x+15\right)}\)
\(=\dfrac{20\left(x^2+6x+9\right)}{\left(3x+5+2x\right)\left(3x+5-2x\right)}+\dfrac{5\left(x-5\right)\left(x+5\right)}{\left(3x-2x-5\right)\left(3x+2x+5\right)}-\dfrac{\left(2x+3-x\right)\left(2x+3+x\right)}{3\left(x+3\right)\left(x+5\right)}\)
\(=\dfrac{20\left(x+3\right)^2}{5\left(x+1\right)\cdot\left(x+5\right)}+\dfrac{5\left(x-5\right)\left(x+5\right)}{5\left(x+1\right)\left(x-5\right)}-\dfrac{\left(x+3\right)\cdot3\left(x+1\right)}{3\left(x+3\right)\left(x+5\right)}\)
\(=\dfrac{4\left(x+3\right)^2}{\left(x+1\right)\left(x+5\right)}+\dfrac{x+5}{x+1}-\dfrac{x+1}{x+5}\)
\(=\dfrac{4\left(x+3\right)^2+\left(x+5\right)^2-\left(x+1\right)^2}{\left(x+1\right)\left(x+5\right)}\)
\(=\dfrac{4x^2+24x+36+x^2+10x+25-x^2-2x-1}{\left(x+1\right)\cdot\left(x+5\right)}\)
\(=\dfrac{4x^2+32x+60}{\left(x+1\right)\left(x+5\right)}=\dfrac{4\left(x^2+8x+15\right)}{\left(x+1\right)\left(x+5\right)}\)
\(=\dfrac{4\left(x+3\right)\cdot\left(x+5\right)}{\left(x+1\right)\left(x+5\right)}=\dfrac{4x+12}{x+1}\)
VT
0