Cho có AB = AC. Trên cạnh AB lấy điểm E, trên cạnh AC lấy điểm D sao cho AD =AE.
a. Chứng minh tam giác ADB = tam giác AEC từ đó so sánh góc ABD và gócACE
b. Gọi O là giao điểm của BD và CE chứng minh ;
c. Chứng minh AO là đường trung trực của DE.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét △ AED có AE=AD nến △AED cân tại A
⇒\(\widehat{AED}=\widehat{ADE}\) ⇒\(\widehat{DEB}=\widehat{EDC}\)
△ABC cân ⇒AB=AC mà AE=AD⇒EB=DC
Xét △DEB và △EDC có :
\(\widehat{DEB}=\widehat{EDC}\left(cmt\right)\)
ED : cạnh chung
EB=DC \(\left(cmt\right)\)
Do đó : △DEB = △EDC \(\left(c.g.c\right)\)
Nên \(\widehat{EBD}=\widehat{DCE}\) hay \(\widehat{ABD}=\widehat{ACE}\)
b) △ABC cân ⇒\(\widehat{ABC}=\widehat{ACB}\) mà \(\widehat{ABD}=\widehat{ACE}\) (câu a) ⇒\(\widehat{IBC}=\widehat{ICB}\)
Vậy △IBC cân tại I
c) Xét △AIB và △AIC có :
AB=AC(gt)
\(\widehat{ABD}=\widehat{ACE}\) (câu a)
BI=CI(vì △IBC cân tại I)
Do đó :△AIB=△AIC\(\left(c.g.c\right)\)
⇒\(\widehat{BAI}=\widehat{CAI}\) ⇒ AI là tia phân giác \(\widehat{BAC}\)
d) Xét △AED và △ABC có :
A : chung
\(\dfrac{AE}{AB}=\dfrac{AD}{AC}\)
Nên △AED đồng dạng △ABC \(\left(c.g.c\right)\)
⇒\(\widehat{AED}=\widehat{ABC}\) ⇒ ED//BC
Vì AI là đường phân giác của △AED mà △AED cân nên AI cũng là đường cao ⇒AI⊥ED lại có : ED//BC ⇒AI⊥BC
e) AI⊥BC (AI là đường cao tam giác ABC) mà △ABC cân nên AI cũng là đường trung tuyến ⇒ AI là đường trung trực của BC
a, Xét tam giác ABD và tam giác ACE ta có :
^A _ chung
^AB = AC ( gt )
AD = AE ( gt )
Vậy tam giác ABD = tam giác ACE ( g.c.g )
b, => ^ABD = ^ACE ( 2 góc tương ứng )
mà tam giác ABC cân tại => ^B = ^C
=> ^B - ^ABD = ^DBC
=> ^C - ^ACE = ^ECB
=> ^DBC = ^ECB
Xét tam giác IBC có : ^DBC = ^ECB
nên IBC là tam giác cân tại I
c, Xét tam giác ABI và tam giác ACI ta có :
^ABI = ^ACI ( cmt )
AB = AC ( gt)
IA _ chung
Vậy tam giác ABI = tam giác ACI ( c.g.c )
=> ^BAI = ^CAI ( 2 góc tương ứng )
Vậy AI là phân giác ^BAC
d, Ta có : \(\dfrac{AE}{AB}=\dfrac{AD}{AC}\)=> ED // BC ( Ta lét đảo )
mà AI là phân giác của tam giác ABC cân tại A
=> AI đồng thời là đường cao
=> AI vuông BC ; ED // BC (cmt)
=> AI vuông ED
e, Xét tam giác ABC cân tại A
AI là đường cao, phân giác
đồng thời AI là đường trung trực đoạn BC

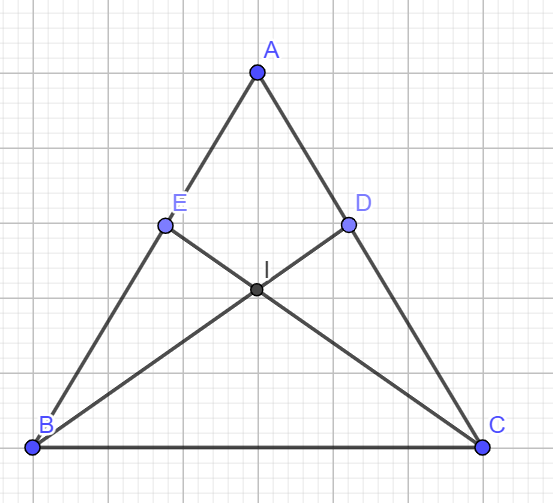
a)∆ABD và ∆ACE có:
AB=AC(gt)
Góc A là góc chung.
AD=AE(gt)
Nên ∆ABD=∆ACE(c.g.c)
Suy ra: Góc ABD=góc ACE( 2 góc tương ứng)
Vậy Góc ABD=góc ACE
b) Ta cóGóc ABD=góc ACE
mà góc ABC =góc ACB( do tam giác ABC cân tại A)
suy ra Góc IBC=góc ICB
=>Tam giác IBC cân tại I
Vậy ∆IBC cân tại I

a: Xét ΔABD và ΔACE có
AB=AC
\(\widehat{A}\) chung
AD=AE
Do đó: ΔABD=ΔACE
Suy ra \(\widehat{ABD}=\widehat{ACE}\)
b:Xét ΔEBC và ΔDCB có
EB=DC
BC chung
EC=DB
Do đó: ΔEBC=ΔDCB
Suy ra: \(\widehat{ICB}=\widehat{IBC}\)
hay ΔIBC cân tại I
=>IB=IC
Ta có: EI+CI=EC
DI+BI=BD
mà BD=CE
và IB=IC
nên ID=IE

a: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là tia phân giác
a: Xét ΔADB và ΔAEC có
AD=AE
\(\widehat{A}\) chung
AB=AC
Do đó: ΔADB=ΔAEC