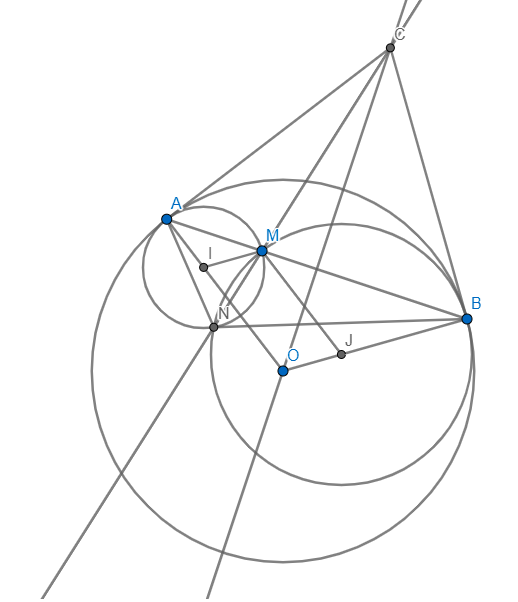
cho đường tròn O bán kính R, dây AB cố định. Điểm M thuộc cung lớn AB. Gọi I là trung điểm của dây AB. Vẽ đường tròn tâm O' qua M tiếp xúc với AB tại A. Tia MI cắt đường tròn tâm o' tại N và cắt đường tròn tâm O tại C. cm NA song sonh với BC?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Xét (O'): \(O'A\perp AB\) tại A và O'A là bán kính.
\(\Rightarrow\)AB là tiếp tuyến của (O') tại A.
\(\Rightarrow\widehat{NAB}\) là góc tạo bởi tiếp tuyến và dây cung chắn cung AN.
Mặt khác \(\widehat{AMN}\) là góc nội tiếp chắn cung AN.
\(\Rightarrow\widehat{AMN}=\widehat{NAB}\left(1\right)\)
Xét (O): \(\widehat{AMC}=\widehat{ABC}\left(=\dfrac{1}{2}sđ\stackrel\frown{AC}\right)\left(2\right)\)
\(\left(1\right),\left(2\right)\Rightarrow\widehat{NAB}=\widehat{ABC}\) nên AN//BC.

Mình không vẽ hình được mong bạn thông cảm
a, Vì tứ giác MANB nội tiếp
=>\(IN.IM=IA.IB=IA^2\)(I là trung điểm của AB)
Vậy IN.IM=IA^2
b,
VÌ AB là tiếp tuyến chắn cung AP của đường tròn O'
=>PAB=AMP
MÀ AMP=ABN (tứ giác AMBN nội tiếp)
=>PAB=ABN
MÀ I là trung điểm của AB
=> I là trung điểm của NP
=> tứ giác ANBP là hình bình hành
Vậy tứ giác ANBP là hình bình hành
c,Vì tứ giác ANBP là hình bình hành
nên \(AN//BP\)
=>NAB=ABP
Lại có NAB=NMB( tứ giác AMBN nội tiếp)
=>ABP=NMB
=> IB là tiếp tuyến của đường tròn ngoại tiếp tam giác MBP
Vậy IB là tiếp tuyến của đường tròn ngoại tiếp tam giác MBP
d,Từ G kẻ GK,GH lần lượt song song với AP,BP(\(K,H\in AB\))
=> \(\hept{\begin{cases}IK=\frac{1}{3}IA\\IH=\frac{1}{3}IB\end{cases}}\)và KGH=APB
MÀ I,A,B cố định
=> H,K cố định
Ta có APB=KGH
Mà APB =ANB( tứ giác ANBP là hbh)
=> KGH=ANB
MÀ AB cố định ,ANB là góc nội tiếp chắn cung AB =
=> ANB không đổi => KGH không đổi
MÀ K,H cố định
=> G thuộc cung tròn cố định
Vậy khi M di chuyển thì G thuộc cung tròn cố định

a) Tiếp tuyến tại A và B của (O) cắt nhau tại C.CM cắt (I) tại N'
Xét \(\Delta CAM\) và \(\Delta CN'A:\) Ta có: \(\left\{{}\begin{matrix}\angle ACN'chung\\\angle CAM=\angle CN'A\end{matrix}\right.\)
\(\Rightarrow\Delta CAM\sim\Delta CN'A\left(g-g\right)\Rightarrow\dfrac{CA}{CN'}=\dfrac{CM}{CA}\Rightarrow CA^2=CM.CN'\)
mà \(CA^2=CB^2\Rightarrow CB^2=CM.CN'\Rightarrow\dfrac{CB}{CM}=\dfrac{CN'}{CB}\)
Xét \(\Delta CBM\) và \(\Delta CN'B:\) Ta có: \(\left\{{}\begin{matrix}\angle BCN'chung\\\dfrac{CB}{CM}=\dfrac{CN'}{CB}\end{matrix}\right.\)
\(\Rightarrow\Delta CBM\sim\Delta CN'B\left(c-g-c\right)\Rightarrow\angle CBB=\angle CN'B\Rightarrow N'\in\left(J\right)\)
\(\Rightarrow N\equiv N'\Rightarrow MN\) luôn đi qua điểm C mà A,B cố định
\(\Rightarrow C\) cố định \(\Rightarrow\) đpcm
b) mình chỉ chứng minh được N thuộc 1 đường tròn cố định thôi,còn chạy trên đoạn thẳng hình như là ko được
Ta có: \(\angle ANB=\angle ANM+\angle BNM=\dfrac{1}{2}\angle AIM+\dfrac{1}{2}\angle BJM\)
Xét \(\Delta AIM\) và \(\Delta AOB:\) Ta có: \(\left\{{}\begin{matrix}\angle OABchung\\\dfrac{IA}{OA}=\dfrac{IM}{OB}\end{matrix}\right.\)
\(\Rightarrow\Delta AIM\sim\Delta AOB\left(c-g-c\right)\Rightarrow\angle AIM=\angle AOB\)
Tương tự \(\Rightarrow\angle BJM=\angle AOB\)
\(\Rightarrow\angle ANB=\dfrac{1}{2}\angle AOB+\dfrac{1}{2}\angle AOB=\angle AOB\)
\(\Rightarrow N\in\left(AOB\right)\) mà A,O,B cố định \(\Rightarrow N\in\left(AOB\right)\) cố định