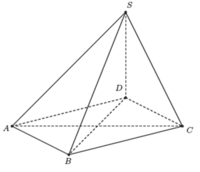
cho hình chóp s.abc có sa=sb=sc=a và tam giác abc đều cạnh \(a\sqrt{2}\). tính cosin góc giữa SC và AB?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án C
Gọi O là trung điểm của BC, suy ra O là tâm đường tròn ngoại tiếp tam giác ABC.
Ngoài ra, theo giả thiết ta có SA = SB = SC nên SO là trục của đường tròn ngoại tiếp tam giác ABC.
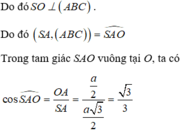
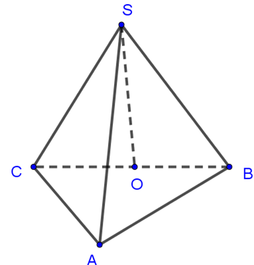

a: SO vuông góc (ABC)
=>(SGO) vuông góc (ABC)
b: ((SAB);(ABC))=(SG;AG)=góc SGA
\(AG=\dfrac{a\sqrt{3}}{3}\)
cos SGA=AG/SA=căn 3/3:2=căn 3/6
=>góc SGA=73 độ

a: \(\widehat{SB;AB}=\widehat{SBA}\)
SA\(\perp\)(ABC)
=>\(SA\perp AB;SA\perp AC;SA\perp BC\)
Xét ΔSAB vuông tại A có \(tanSBA=\dfrac{SA}{AB}=\dfrac{a\sqrt{3}}{a}=\sqrt{3}\)
=>\(\widehat{SBA}=60^0\)
=>\(\widehat{SB;AB}=60^0\)
b:
\(\widehat{SC;AC}=\widehat{SCA}\)
Xét ΔSAC vuông tại A có \(tanSCA=\dfrac{SA}{AC}=\dfrac{a\sqrt{3}}{a}=\sqrt{3}\)
nên \(\widehat{SCA}=60^0\)
=>\(\widehat{SC;AC}=60^0\)
c: ΔABC đều có AM là đường trung tuyến
nên \(AM=BC\cdot\dfrac{\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{2}\)
Ta có: SA\(\perp\)(ABC)
AM\(\subset\)(ABC)
Do đó: SA\(\perp\)AM
=>ΔSAM vuông tại A
\(\widehat{SM;AM}=\widehat{SMA}\)
Xét ΔSMA vuông tại A có \(tanSMA=\dfrac{SA}{AM}=\dfrac{a\sqrt{3}}{\dfrac{a\sqrt{3}}{2}}=2\)
=>\(\widehat{SMA}\simeq63^026'\)
=>\(\widehat{SM;AM}\simeq63^026'\)
a.
Góc giữa SB và AB là góc \(\widehat{SBA}\)
Trong tam giác vuông SAB:
\(tan\widehat{SBA}=\dfrac{SA}{AB}=\dfrac{a\sqrt{3}}{a}=\sqrt{3}\)
\(\Rightarrow\widehat{SBA}=60^0\)
b.
Góc giữa SC và AC là góc \(\widehat{SCA}\)
\(tan\widehat{SCA}=\dfrac{SA}{AC}=\sqrt{3}\Rightarrow\widehat{SCA}=60^0\)
c.
Góc giữa SM và AM là góc \(\widehat{SMA}\)
AM là trung tuyến tam giác đều \(\Rightarrow AM=\dfrac{a\sqrt{3}}{2}\)
\(\Rightarrow tan\widehat{SMA}=\dfrac{AM}{SA}=2\Rightarrow\widehat{SMA}=60^026'\)

Đáp án D
Phương pháp: Góc giữa đường thẳng và mặt phẳng là góc giữa đường thẳng và hình chiếu của nó trên mặt phẳng đó.
Cách giải: Gọi H là trung điểm của AC
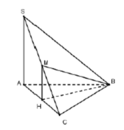
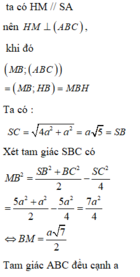
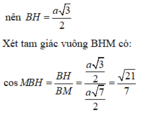

Đáp án B
Gọi D là hình chiếu của S trên (ABC). Khi đó S D ⊥ A B C .
Do đó hình chiếu của SC trên (ABC) là CD. Suy ra góc giữa SC và (ABC) là S C D ^ .
Ta có B C ⊥ S C B C ⊥ S D ⇒ B C ⊥ C D , A B ⊥ S A A B ⊥ S D ⇒ A B ⊥ A D .
Vậy ABCD là hình chữ nhật.
Theo đề S C D ^ = 60 0 . Ta tính được B D = A C = a 5 , D S = C D 3 = a 3 .
Vậy S B = S D 2 + B D 2 = 8 a 2 = 2 a 2 .

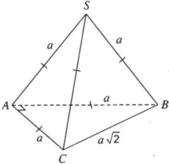
Ta tính côsin của góc giữa hai vectơ S C → và A B → . Ta có
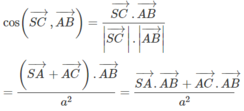
Theo giả thiết ta suy ra hình chóp có các tam giác đều là SAB, SAC và các tam giác vuông là ABC vuông tại A và SBC vuông tại S.
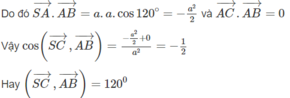
Vậy góc giữa hai vectơ A B → v à S C → bằng 120 o .

a)
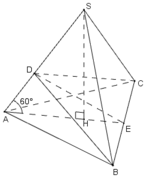
+ Gọi H là hình chiếu của S trên (ABC)
⇒ AH là hình chiếu của SA trên (ABC)
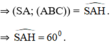
Gọi E là trung điểm BC
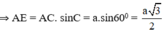
H là tâm của Δ đều ABC.



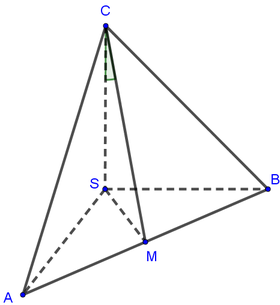
ông này khuya rồi đăng bài nhiều d :(((
vẫn hình vẽ ấy lập luận tương tự
Gọi M là trung điểm của AB ta có:
AB _|_ SM ( tam giác SAB cân tại S ) (1)
AB _|_ CM ( tam giác ABC đều ) (2)
Từ (1),(2) suy ra AB vuông góc SCM
suy ra góc (AB,SC)=90