Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Đáp án C
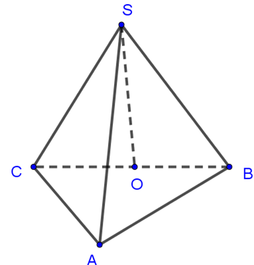
Gọi O là trung điểm của BC, suy ra O là tâm đường tròn ngoại tiếp tam giác ABC.
Ngoài ra, theo giả thiết ta có SA = SB = SC nên SO là trục của đường tròn ngoại tiếp tam giác ABC.
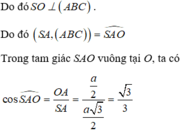

Đáp án B
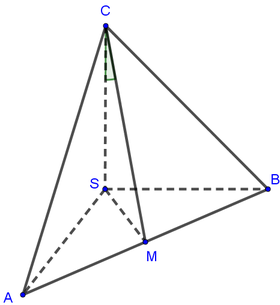
c os S M ; B C = c os S M → ; B C → = S M → . B C → S M . B C , ta có S M = a 2 2 ; B C = a 2 ;
S
M
→
.
B
C
→
=
1
2
S
B
→
+
S
A
→
S
C
→
−
S
B
→
=
−
1
2
S
B
2
=
−
1
2
a
2
;
c
os
S
M
;
B
C
^
=
1
2
⇒
S
M
;
B
C
^
=
60
∘

Chọn A
Chọn hệ trục tọa độ A(1;0;0), B(0;2;0), C(0;0;3).
Khi đó M thuộc mặt phẳng (ABC) thỏa mãn đề bài nên S M = 6 3 11

Đáp án C
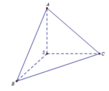
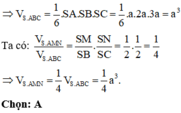
Thể tích khối chóp S.ABC là
V = 1 6 S A . S B . S C = 1 6 .2 3 .2.3 = 2 3

Đáp án D
Phương pháp:
- Gọi H là trực tâm tam giác, chứng minh S H ⊥ A B C bằng cách sử dụng định lý: “Đường thẳng vuông góc với hai đường thẳng cắt nhau thì nó vuông góc với mặt phẳng chứa hai đường thẳng đó”.
- Tính độ dài SH bằng cách sử dụng hệ thức lượng giữa cạnh và đường cao trong tam giác vuông.
Cách giải: Gọi H là trực tâm của tam giác ABC.
Ta sẽ chứng minh SH là đường cao của hình chóp.
Gọi E, D lần lượt là hình chiếu của B,A lên AC,BC.


Chú ý khi giải: Từ nay về sau, các em có thể ghi nhớ hệ thức liên hệ giữa đường cao và cạnh trong hình chóp S.ABC mà có SA, SB, SC đôi một vuông góc, đó là 1 S H 2 = 1 S A 2 1 S B 2 + 1 S C 2

Phương pháp:
+) Thể tích của tứ diện vuông có độ dài các cạnh góc vuông là a, b, c là: V = 1 6 a b c
+) Sử dụng công thức tỉ số thể tích Simpson
Cách giải:
S.ABC là tứ diện vuông tại đỉnh S