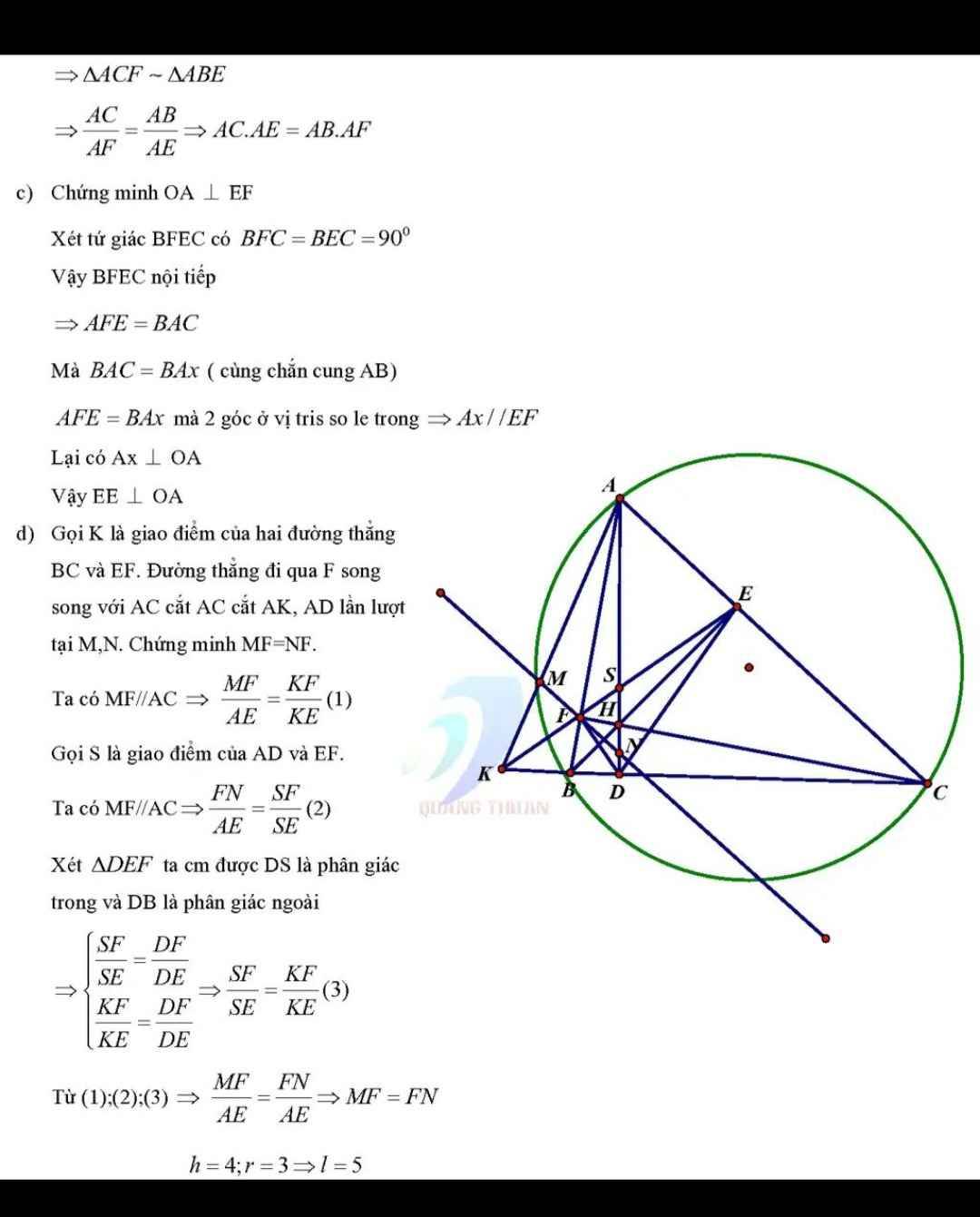
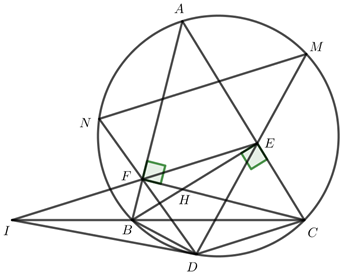
Cho tam giác ABC nhọn (AB>AC) nội tiếp đường tròn (O). BE,CF là đường cao của tam giác ABC cắt nhau tại H (E∈AC, F∈AB), K là giao điểm của hai đường thẳng EF và BC. Đoạn thẳng KA cắt (O) tại M. Gọi I là trung điểm của BC. Chứng minh rằng:
1) Tứ giác BCEF nội tiếp
2) KE.KF=KM.KA
3) Ba điểm M,H,I thẳng hàng