Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


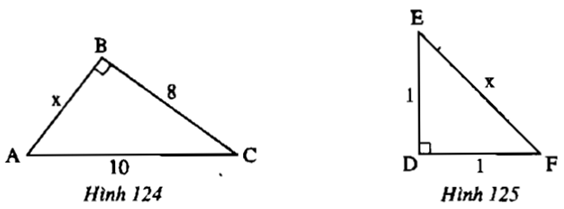
Áp dụng định lí Py – ta – go
Tam giác ABC vuông tại B
⇒ x2 + 82 = 102
⇒ x2 = 102 – 82 = 36
⇒ x = 6 (cm)
Tam giác DEF vuông tại D
⇒ 12 + 12 = x2
⇒ x2 = 1 + 1 = 2
⇒ x = √2 (cm)

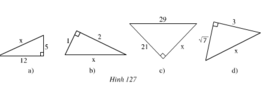
- Hình a
Áp dụng định lí Pi-ta-go ta có:
x2 = 122 + 52 = 144 + 25 = 169 ⇒ x = 13
- Hình b
Ta có: x2 = 12 + 22 = 1 + 4 = 5
⇒ x = √5
- Hình c
Theo định lí Pi-ta-go 292 = 212 + x2
Nên x2 = 292 - 212 = 841 - 441 = 400
⇒ x = 20
- Hình d
Theo định lí Pi-ta-go ta có:
x2 = (√7)2 + 32 = 7 + 9 = 16
⇒ x = 4

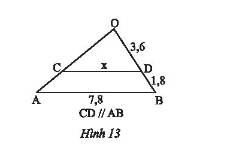
Trong tam giác \(OAB\) có \(CD//AB\).
Theo hệ quả của định lí Thales ta có:
\(\frac{{OD}}{{OB}} = \frac{{CD}}{{AB}}\) mà \(OB = OD + DB = 3,6 + 1,8 = 5,4\)
Suy ra, \(\frac{{3,6}}{{5,4}} = \frac{x}{{7,8}} \Rightarrow x = \frac{{3,6.7,8}}{{5,4}} = 5,2\).
Vậy \(x = 5,2\).

Xét tam giác ABC có:
\(\begin{array}{l}\widehat {BAC} + \widehat {ABC} + \widehat C = {180^o}\\ \Rightarrow {45^o} + y + {75^o} = {180^o}\\ \Rightarrow y = {60^o}\end{array}\)
Xét tam giác ABD có:
\(\begin{array}{l}\widehat {DAB} + \widehat {DBA} + \widehat D = {180^o}\\ \Rightarrow x + {60^o} + {75^o} = {180^o}\\ \Rightarrow x = {45^o}\end{array}\)
Xét 2 tam giác ABC và ABD có:
\(\widehat {CAB} = \widehat {DAB} (= {45^o})\)
AB chung
\(\widehat C = \widehat D (= {75^o})\)
=>\(\Delta ABC = \Delta ABD\)(g.c.g)
=> BC=BD ( 2 cạnh tương ứng), mà BD = 3,3 cm => a= BC= 3,3 cm.
AC=AD ( 2 cạnh tương ứng), mà AC = 4 cm => b = AD = 4cm.

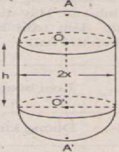
Ta có: AA’ = AO + OO’ + O’A’
hay 2a = x + h + x
hay 2x + h = 2a.

Trong tam giác ABC, ta có: MN // BC
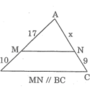
Suy ra: 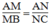
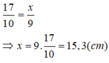
Trong tam giác PQR, ta có: EF // QR
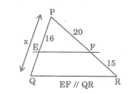
Suy ra: 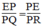
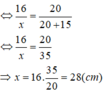


a) Biểu thức biểu thị:
- Diện tích hình vuông có độ dài cạnh là x cm là \(x.x = {x^2}(c{m^2})\)
- Thể tích của hình lập phương có độ dài cạnh là 2x cm là \({(2x)^3} = 8{x^3}(c{m^3})\)
b) Các biểu thức trên có dạng một biến với lũy thừa có số mũ nguyên dương của biến đó.
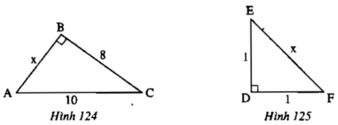
Hình 124Theo định lí Pi-ta-go ta có:AC^2-BC^2=AB^2⇒10^2-8^2=AB^2⇒100-64=AB^2⇒36=AB^2⇒AB=6 (Vì AB>0)Hình 125Theo định lí Pi-ta-go ta có:DE^2+DF^2=EF^2⇒1^2+1^2=EF^2⇒1+1=EF^2⇒2=EF^2⇒EF=2 (vì EF>0)