Cho hàm số y = \(\dfrac{\left(3m+1\right)x-m^2+m}{x+m}\) trong đó m là tham số khác 0. Gọi S là tập hợp các giá trị thực của m để tại giao điểm của đồ thị với trục hoành, tiếp tuyến sẽ vuông góc với đường thẳng x+y-2020 = 0. Khi đó tổng giá trị các phần tử thuộc S bằng
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
24 tháng 9 2018
Đáp án D
Ta có y ' = 4 x 3 − 4 m + 1 x ⇒ y ' 1 = 4 − 4 m + 1 = − 4 m = k Δ là hệ số góc của PTTT tại A
Δ ⊥ d ⇒ k Δ . k d = − 1 ⇔ − 4 m 1 4 = − 1 ⇔ m = 1
22 tháng 12 2023
a: Thay x=1 và y=-1 vào (d), ta được:
\(\left(m-2\right)\cdot1+m+1=-1\)
=>m-2+m+1=-1
=>2m-1=-1
=>2m=0
=>m=0
b: Thay y=0 vào y=x+2, ta được:
x+2=0
=>x=-2
Thay x=-2 và y=0 vào y=(m-2)x+m+1, ta được:
-2(m-2)+m+1=0
=>-2m+4+m+1=0
=>5-m=0
=>m=5
2 tháng 7 2023
x^2+(y-1)^2=4
=>R=2 và I(0;1)
A(1;1-m) thuộc (C)
y'=4x^3-4mx
=>y'(1)=4-4m
PT Δsẽ là y=(4-m)(x-1)+1-m
Δ luôn đi qua F(3/4;0) và điểm F nằm trong (λ)
Giả sử (Δ) cắt (λ) tại M,N
\(MN=2\sqrt{R^2-d^2\left(I;\Delta\right)}=2\sqrt{4-d^2\left(I;\Delta\right)}\)
MN min khi d(I;(Δ)) max
=>d(I;(Δ))=IF
=>Δ vuông góc IF
Khi đó, Δ có 1 vecto chỉ phương là: vecto u vuông góc với vecto IF=(3/4;p-1)
=>vecto u=(1;4-4m)
=>1*3/4-(4-4m)=0
=>m=13/16
CM
18 tháng 4 2017
Chọn đáp án D
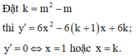
Đồ thị hàm số có hai điểm cực trị khi và chỉ khi k ≠ 1
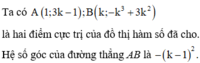
Đường thẳng AB vuông góc với đường thẳng y = x + 2 khi và chỉ khi
CM
30 tháng 11 2019
Đáp án A
Điều kiện: x ≠ 2. Do M là giao điểm của đồ thị hàm số y = x + 1 x − 2 với trục hoành nên M − 1 ; 0
Ta có y ' = − 3 x − 2 2 nên hệ số góc của tiếp tuyến tại M là k = y ' − 1 = − 1 3
Do đó suy ra phương trình tiếp tuyến là y = − 1 3 x − 1 3 x + 3 y + 1
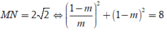
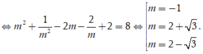
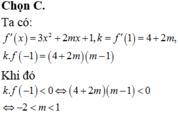
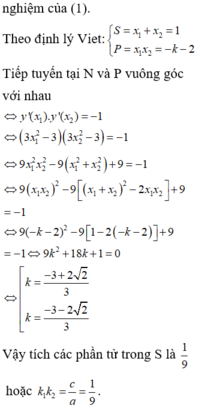
Tiếp tuyến có hệ số góc bằng 1
\(y'=\dfrac{m\left(3m+1\right)-\left(-m^2+m\right)}{\left(x+m\right)^2}=\dfrac{4m^2}{\left(x+m\right)^2}\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{m^2-m}{3m+1}\\\dfrac{4m^2}{\left(x+m\right)^2}=1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{m^2-m}{3m+1}\\\left[{}\begin{matrix}2m=x+m\\-2m=x+m\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{m^2-m}{3m+1}\\\left[{}\begin{matrix}x=m\\x=-3m\end{matrix}\right.\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}m=\dfrac{m^2-m}{3m+1}\\-3m=\dfrac{m^2-m}{3m+1}\end{matrix}\right.\)
\(\Leftrightarrow...\)