cho hình chóp S.ABCD có đáy ABCD là hình bình hành .Gọi O là giao điểm của AC và BD .M và N lần lượt là trung điểm của CD và SA . G là trọng tâm tam giác SAB .Gọi \(\Delta\) là giao tuyến của 2 mặt ph...

LL

Linh Lê

6 tháng 1 2021

cho hình chóp S.ABCD có đáy ABCD là hình bình hành .Gọi O là giao điểm của AC và BD .M và N lần lượt là trung điểm của CD và SA . G là trọng tâm tam giác SAB .Gọi \(\Delta\) là giao tuyến của 2 mặt phẳng (SAD) và (SMG),P là giao điểm của đường thẳng OG và \(\Delta\) .Chứng minh P,N ,D thẳng...

Đọc tiếp

#Toán lớp 11

0

NM

NGUYỄN MINH HUY

22 tháng 12 2020

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi G là trọng tâm của tam giác SAB; I và M lần lượt là trung điểm của AB và SD. a) Tìm giao tuyến của hai mặt phẳng (SAB) và (SCD) b) Gọi N là giao điểm DI và AC. Chứng minh rằng NG song song với (SCD) c)Tìm giao điểm E của SO và (CGM). Tính tỉ...

Đọc tiếp

#Toán lớp 11

1

HT

Hoàng Tử Hà

22 tháng 12 2020

Hình câu c là tui vẽ riêng ra cho dễ nhìn thôi, còn hình vẽ trình bày vô bài lấy hình chung ở câu a và b nhó :v

undefined

Đúng(1)

NM

NGUYỄN MINH HUY

23 tháng 12 2020

cảm ơn bạn nha

Đúng(0)

PT

Pham Trong Bach

9 tháng 8 2018

Cho hình chóp S.ABCD với đáy ABCD là hình bình hành. Gọi lần lượt là trọng tâm của các tam giác SAD và SBC. Gọi M là giao điểm của SG và AD; N là giao điểm của SG’ và BC và O là giao điểm của BD và AN. Tìm giao tuyến của mặt phẳng (ADG’) và (SBD) A. DI trong đó I là giao điểm của SO và AG’ B. DJ trong đó J là giao điểm của AG’ và SD C. DH trong đó H là giao điểm của AD và BD D. Tất cả...

Đọc tiếp

#Toán lớp 11

1

CM

Cao Minh Tâm

9 tháng 8 2018

Đúng(0)

NM

Nguyễn Minh Huy

22 tháng 12 2020 - olm

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi G là trọng tâm của tam giác SAB; I và M lần lượt là trung điểm của AB và SD.

a) Tìm giao tuyến của hai mặt phẳng (SAB) và (SCD)

b) Gọi N là giao điểm DI và AC. Chứng minh rằng NG song song với (SCD)

c)Tìm giao điểm E của SO và (CGM). Tính tỉ số \(\frac{SE}{SO}\)

#Toán lớp 11

0

PT

Pham Trong Bach

25 tháng 3 2017

Cho hình chóp S.ABCD có đáy ABCD là hình thang, AB // CD. Gọi M, N lần lượt là trung điểm của AD và BC; gọi G là trọng tâm tam giác SAB. Thiết diện của hình chóp với mặt phẳng (MNG) là hình bình hành thì A. AB = 3CD B. AB = 2CD C. CD = 3AB D. CD =...

Đọc tiếp

#Toán lớp 11

1

CM

Cao Minh Tâm

25 tháng 3 2017

Chọn A

Đúng(0)

PT

Pham Trong Bach

29 tháng 1 2019

Cho hình chóp S.ABCD có đáy ABCD là hình thang, AB//CD. Gọi M, N lần lượt là trung điểm của AD và BC; gọi G là trọng tâm tam giác SAB. Thiết diện của hình chóp với mặt phẳng (MNG) là hình bình hành thì A. AB = 3CD B. AB = 2CD C. CD = 3AB D. CD =...

Đọc tiếp

#Mẫu giáo

1

CM

Cao Minh Tâm

29 tháng 1 2019

Đúng(0)

NN

nguyen ngoc son

20 tháng 9 2023

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi H và K

lần lượt là trung điểm của SA và SC, G là trọng tâm của tam giác ABC.

a) Tìm giao tuyến của (GHK) và (ABCD).

b) Tìm giao điểm M của SD và (GHK).

c) Gọi E trung điểm của HK. Chứng minh G, E, M thẳng hàng.

#Toán lớp 11

1

NL

Nguyễn Lê Phước Thịnh

28 tháng 10 2023

a: Xét ΔSAC có

H,K lần lượt là trung điểm của SA,SC

=>HK là đường trung bình

=>HK//AC

Xét (GHK) và (ABCD) có

HK//AC
\(G\in\left(GHK\right)\cap\left(ABCD\right)\)

Do đó: (GHK) giao (ABCD)=xy, xy đi qua G và xy//HK//AC

b: Chọn mp(SBD) có chứa SD

Gọi O là giao điểm của AC và BD

ABCD là hình bình hành

=>AC cắt BD tại trung điểm của mỗi đường

=>O là trung điểm chung của AC và BD

Xét ΔABC có

G là trọng tâm

BO là trung tuyến của ΔABC

Do đó: B,O,G thẳng hàng

=>G\(\in\)BD

Trong mp(SAC), gọi I là giao điểm của SO với HK

\(I\in SO\subset\left(SBD\right);I\in HK\subset\left(GHK\right)\)

=>\(I\in\left(SBD\right)\cap\left(GHK\right)\)(1)

\(G\in BD\subset\left(SBD\right);G\in\left(GHK\right)\)

=>\(G\in\left(SBD\right)\cap\left(GHK\right)\left(2\right)\)

Từ (1) và (2) suy ra \(\left(SBD\right)\cap\left(GHK\right)=GI\)

Gọi M là giao điểm của SD với GI

=>M là giao điểm của SD với (SHK)

c: Xét ΔSAC có

O,K lần lượt là trung điểm của CA,CS

=>OK là đường trung bình của ΔSAC

=>OK//SA và OK=SA/2

OK=SA/2

SH=SA/2

Do đó: OK=SH

Xét tứ giác SHOK có

SH//OK

SH=OK

Do đó: SHOK là hình bình hành

=>HK cắt SO tại trung điểm của mỗi đường

mà E là trung điểm của HK

nên Elà trung điểm của SO

=>E trùng với I

=>(SBD) giao (GHK)=GE

=>G,E,M thẳng hàng

Đúng(0)

TD

Tử Dương

30 tháng 11 2021

Cho hình chóp S.ABCD có đáy là hình thang với các cạnh đáy là AB và CD. Gọi I ,J lần lượt là trung điểm của AD và BC, G là trọng tâm của tam giác SAB. Tìm giao tuyến của hai mặt phẳng (SAB) và (IJG).

#Toán lớp 11

1

HP

Hồng Phúc

4 tháng 12 2021

Gọi \(K=AB\cap IJ\), \(P=KG\cap SB\), \(H=KG\cap SA\)

\(\Rightarrow JIHP\) là thiết diện cần tìm

Đúng(0)

B

Buddy

14 tháng 7 2023

Cho hình chóp S.ABCD có đáy là ABCD là hình bình hành. Lấy điểm M trên cạnh AD sao cho AD=3AM. Gọi G, N lần lượt là trọng tâm của tam giác SAB, ABC.a) Tìm giao tuyến của hai mặt phẳng (SAB) và (SCD).b) Chứng minh rằng MN song song với mặt phẳng (SCD) và NG song song với mặt...

Đọc tiếp

#Toán lớp 11

2

QT

Quoc Tran Anh Le

Giáo viên

22 tháng 8 2023

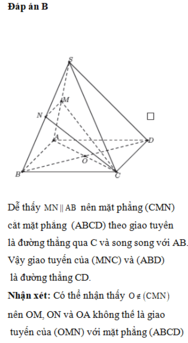
a) S là điểm chung của hai mặt phẳng (SAB) và (SCD) mà AB // CD

Từ S kẻ Sx sao cho Sx // AB // CD nên Sx là giao tuyến của hai mặt phẳng (SAB) và (SCD).

Đúng(0)

QT

Quoc Tran Anh Le

Giáo viên

22 tháng 9 2023

b) Gọi E là trung điểm của AB

G là trọng tâm tam giác SAB nên \(\frac{{EG}}{{SE}} = \frac{1}{3}\)

N là trọng tâm tam giác ABC nên\(\frac{{EN}}{{EC}} = \frac{1}{3}\)

Theo Ta lét, suy ra GN // SC mà SC \( \subset \) (SAC). Do đó, GN // (SAC)

Đúng(0)

PT

Pham Trong Bach

22 tháng 9 2017

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N lần lượt là trung điểm của SA, SB. Giao tuyến của (MNC) và (ABD) là:

A. OM

B. CD

C. OA

D. ON

#Toán lớp 11

1

CM

Cao Minh Tâm

22 tháng 9 2017

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP