Cho parabol (P) : y = ax2. Dường thẳng (d) : y = -x + m.Tìm a biết rằng (P) đi qua A(2 ; -1) và vẽ (P) vừa tìm được.Tìm m để (P) vừa tìm được tiếp xúc (d) và tìm tọa độ tiếp điểm.Gọi B là giao điểm của (d) ở câu 2 với trục tung. C là điểm đối xứng của A qua trục tung. Chứng tỏ C nằm trên (P) và tam giác ABC vuông cân. Không biết => không cmt linh tinh kẻo người ta lại bảo đã ngu rồi lại...
Đọc tiếp
Cho parabol (P) : y = ax2. Dường thẳng (d) : y = -x + m.
- Tìm a biết rằng (P) đi qua A(2 ; -1) và vẽ (P) vừa tìm được.
- Tìm m để (P) vừa tìm được tiếp xúc (d) và tìm tọa độ tiếp điểm.
- Gọi B là giao điểm của (d) ở câu 2 với trục tung. C là điểm đối xứng của A qua trục tung. Chứng tỏ C nằm trên (P) và tam giác ABC vuông cân.
- Không biết => không cmt linh tinh kẻo người ta lại bảo đã ngu rồi lại còn tỏ ra nguy hiểm ^_^
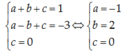
3) tính khoảng cách từ A đến O khoảng cách đó = k/c từ C đến O
suy ra dc: xC2+yC2=5
Mà C là điểm đối xứng của A qua trục tung nên yC=-1
Tìm dc xC thế vào (P) xong 1 nốt nhạt còn 1 nốt nữa
tính từng khoảng cách AB,BC,AC rồi dùng pytago đảo c/m nó vuông
rồi so sánh 2 cgv coi thử nếu = nhau =>nó là t/g vuông cân
đã giỏi còn tỏ ra an toàn hahaha