Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

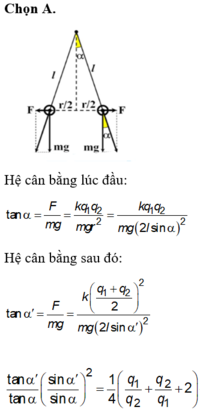
Đáp án A
Hệ cân bằng lúc đầu:
tan α = F m g = k q 1 q 2 m g r 2 = k q 1 q 2 m g 2 ℓ sin α 2
Hệ cân bằng sau đó:
tan α ' = F m g = k q 1 + q 2 2 2 m g 2 ℓ sin α ' 2
tan α ' tan α sin α ' sin α = 1 2 q 1 q 2 + q 2 q 1 + 2 → q 1 q 2 = 7 , 5 q 1 q 2 = 0 , 13


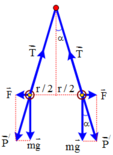
Gọi l là chiều dài của dây treo. Khi chưa trao đổi điện tích với nhau thì khoảng cách giữa hai quả cầu là l. Lực đẩy giữa hai quả cầu là : F 1 = k q 1 q 2 / l 2
Tương tự như ở Hình 1.1 G, ta có : tan 30 ° = (1) với P là trọng lượng quả cầu.
Khi cho hai quả cầu trao đổi điện tích với nhau thì mỗi quả cầu mang điện tích q 1 + q 2 /2. Chúng vẫn đẩy nhau và khoảng cách giữa chúng bây giờ là l 2
Lực đẩy giữa chúng bây giờ là :
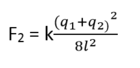
Tương tự như trên, ta có:
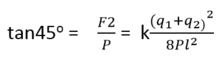 (2)
(2)
Từ (1) và (2) suy ra: 8 3 q 1 q 2 = q 1 + q 2 2
Chia hai vế cho q 2 2 ta có:
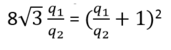
Đặt q 1 / q 2 = x ta có phương trình:
x 2 + (2- 8 3 )x + 1 = 0
hay x 2 - 11,86x + 1 = 0
Các nghiệm của phương trình này là x 1 = 11,77 và x 2 = 0,085
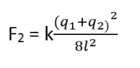

Chọn đáp án A
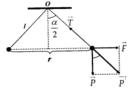
r 2 = l sin α 2 → r 2 r 1 = sin α 2 2 sin α 1 2 = 1 2 1 2 = 2 ⇒ r 2 r 1 2 = 2 1 tan α 1 2 = F 1 P tan α 2 2 = F 2 P ⇒ tan α 1 2 tan α 2 2 = F 1 F 2 = k q 1 q 2 r 1 2 k q 1 + q 2 2 2 r 2 2 → 1 4 q 1 q 2 q 1 + q 2 2 = 1 2 3
Chọn q 1 = 1 → S H I F T − S O L V E q 2 = 0 , 085 ⇒ q 1 q 2 = 11 , 8
Chú ý: ta đã giả sử hai điện tích q 1 và q 2 đều dương
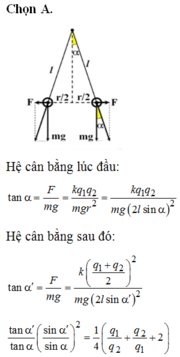

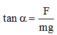
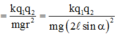
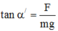
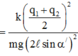
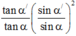
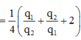


Na ná bài hôm nay tui thi luôn :v
\(F=\dfrac{kq_1q_2}{r^2}\)
Sau khi tiếp xúc, điện tích 2 quả cầu bằng nhau: \(q=\dfrac{\left(q_1+q_2\right)}{2}\Rightarrow F'=\dfrac{k\left(\dfrac{q_1+q_2}{2}\right)^2}{r'^2}=\dfrac{k\left(q_1+q_2\right)^2}{4r'^2}\)
Gọi alpha là góc hợp bởi dây với phương thẳng đứng lúc chưa tiếp xúc, alpha rất nhỏ=> \(\tan\alpha=\sin\alpha=\dfrac{r}{2l}\) \(\Rightarrow r=2l.\tan\alpha\)
\(\tan\alpha=\dfrac{F}{P}\Rightarrow\tan\alpha=\dfrac{kq_1q_2}{r^2.P}=\dfrac{kq_1q_2}{\tan^2\alpha.4l^2.P}\Rightarrow\tan^3\alpha=\dfrac{kq_1q_2}{4l^2.P}\)
Gọi alpha phẩy là góc hợp bởi dây với phương thẳng đứng sau khi tiếp xúc
\(\Rightarrow r'=2l\tan\alpha'\Rightarrow\tan^3\alpha'=\dfrac{k\left(\dfrac{q_1+q_2}{2}\right)^2}{4l^2.P}\)
\(\Rightarrow\dfrac{\tan^3\alpha}{\tan^3\alpha'}=\dfrac{\dfrac{kq_1q_2}{4l^2.P}}{\dfrac{k\left(\dfrac{q_1+q_2}{2}\right)^2}{4l^2.P}}=\dfrac{4q_1q_2}{\left(q_1+q_2\right)^2}\)
Ta luôn có \(\left(q_1+q_2\right)^2\ge4q_1q_2\Rightarrow"="\Leftrightarrow q_1=q_2\Leftrightarrow\alpha=\alpha'\Leftrightarrow r'=r\)