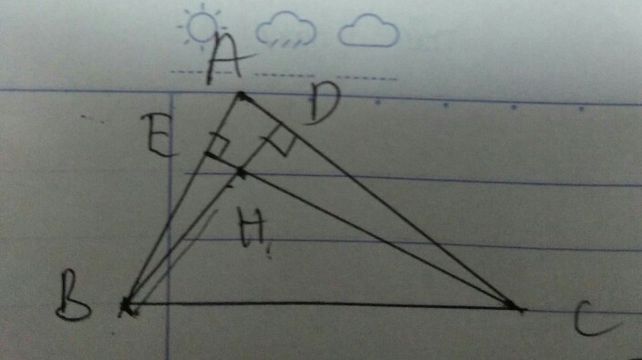
BT1: Cho tam giác nhọn ABC có: AB<AC. Các đường cao BD, CE cắt nhau tại H. I là trung điểm của BC, K là điểm đối xứng với H qua I. M là điểm đối xúng với H qua đường thẳng BC.a) Gọi O là trung điểm AK. CMR: O là giaoo điểm 3 đường trung trực của tam giác ABC.b) Tính tỉ số diện tích của tam giác KIO và tam giác KHA.BT2: Cho hình chữ nhật ABCD: AB>AD. Qua A kẻ đường thẳng vuông góc với BD tại E, cắt CD tại F. Qua C kẻ đường thẳng song song với AF, cắt AB tại K.a) CM: AKCF là hình bình hành.b) CM: Tam giác ADF = tam giác CBK.c) GỌi M, Q lần lượt là trung điểm của AE và BC. Qua M kẻ đường thẳng song song với AD cắt DE tại N. CM: Góc NMB = góc BQN.d) CHo AD= 8cm,Ab=12cm. Tính AE?GIÚP MIK VỚI MIK SẮP THI RÙI!!!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan

6 tháng 10 2021
b: Xét ΔAKB vuông tại K và ΔAKC vuông tại K có
AB=AC
AK chung
Do đó: ΔAKB=ΔAKC
Suy ra: KB=KC
Xét ΔMBK vuông tại M và ΔNCK vuông tại N có
KB=KC
\(\widehat{B}=\widehat{C}\)
Do đó: ΔMBK=ΔNCK
Suy ra: KM=KN(1)
Xét ΔAKB vuông tại K có KM là đường cao ứng với cạnh huyền AB
nên \(AM\cdot MB=KM^2\left(2\right)\)
Xét ΔAKC vuông tại K có KN là đường cao ứng với cạnh huyền AC
nên \(AN\cdot NC=KN^2\left(3\right)\)
Từ (1), (2) và (3) suy ra \(AM\cdot MB=AN\cdot NC\)
HN
0