Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Gọi H là trung điểm của BC
Xét ΔABC có AH là đường trung tuyến
nên \(\overrightarrow{AB}+\overrightarrow{AC}=2\overrightarrow{AH}\)
ΔABC đều có AH là đường trung tuyến
nên \(AH=AB\cdot\dfrac{\sqrt{3}}{2}=3a\cdot\dfrac{\sqrt{3}}{2}\)
=>\(2\cdot AH=3a\sqrt{3}\)
=>\(\left|\overrightarrow{AB}+\overrightarrow{AC}\right|=2\cdot AH=3a\sqrt{3}\)
b:
Gọi I là trung điểm của AH
I là trung điểm của AH
=>\(IA=IH=\dfrac{3a\sqrt{3}}{2}\)
ΔABC đều
mà AH là đường trung tuyến
nên AH vuông góc BC
ΔIHC vuông tại H
=>\(CI^2=HI^2+HC^2\)
=>\(CI^2=\left(\dfrac{3a\sqrt{3}}{2}\right)^2+\left(1,5a\right)^2=9a^2\)
=>CI=3a
\(\left|\overrightarrow{CA}-\overrightarrow{HC}\right|=\left|\overrightarrow{CA}+\overrightarrow{CH}\right|\)
\(=\left|2\cdot\overrightarrow{CI}\right|=2CI\)
\(=2\cdot3a=6a\)

Gọi O là trung điểm của AM
BM=BC/2=a/2
\(\Leftrightarrow AM=\dfrac{a\sqrt{3}}{2}\)
\(\Leftrightarrow MO=\dfrac{a\sqrt{3}}{4}\)
Xét ΔOMB vuông tại M có
\(BO^2=OM^2+BM^2\)
\(=a^2\cdot\dfrac{3}{16}+a^2\cdot\dfrac{1}{4}=a^2\cdot\dfrac{7}{16}\)
\(\Leftrightarrow BO=\dfrac{a\sqrt{7}}{4}\)
Xét ΔBMA có BO là đường trung tuyến
nên \(\overrightarrow{BM}+\overrightarrow{BA}=2\cdot\overrightarrow{BO}\)
\(\Leftrightarrow\left|\overrightarrow{BM}+\overrightarrow{BA}\right|=\dfrac{a\sqrt{7}}{2}\)

\(\overrightarrow{u}=\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GM}+\overrightarrow{GN}=\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}+\overrightarrow{CM}+\overrightarrow{GB}+\overrightarrow{BN}\)
\(=\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}+\overrightarrow{GB}+\overrightarrow{CM}+\overrightarrow{BN}=\overrightarrow{GB}+2\overrightarrow{BN}\)
G là trọng tâm \(\Rightarrow BG=\dfrac{2}{3}.\dfrac{a\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{3}\)
\(\left|\overrightarrow{u}\right|=\left|\overrightarrow{GB}+2\overrightarrow{BN}\right|\Rightarrow\left|\overrightarrow{u}\right|^2=BG^2+4BN^2+4\overrightarrow{GB}.\overrightarrow{BN}\)
\(=\dfrac{a^2}{3}+4a^2+4.\dfrac{a\sqrt{3}}{3}.a.cos120^0=\dfrac{13-2\sqrt{3}}{3}a^2\)
\(\Rightarrow\left|\overrightarrow{u}\right|=\sqrt{\dfrac{13-2\sqrt{3}}{3}}.a\)

I là trung điểm BC \(\Rightarrow\overrightarrow{BI}=\dfrac{1}{2}\overrightarrow{BC}=\dfrac{1}{2}\overrightarrow{AD}\Rightarrow2\overrightarrow{BI}=\overrightarrow{AD}\)
\(\overrightarrow{u}=2\left(\overrightarrow{AB}+\overrightarrow{BI}\right)-3\overrightarrow{AD}=2\overrightarrow{AB}+2\overrightarrow{BI}-3\overrightarrow{AD}=2\overrightarrow{AB}-2\overrightarrow{AD}=2\left(\overrightarrow{AB}+\overrightarrow{DA}\right)=2\overrightarrow{DB}\)
\(\Rightarrow\left|\overrightarrow{u}\right|=2\left|\overrightarrow{DB}\right|=2DB=2a\sqrt{2}\)
em thưa thầy em chưa hiểu đoạn 2AB+2BI-3AD tại sao ra 2AB-2AD ạ

Dựng hình bình hành ABDC.
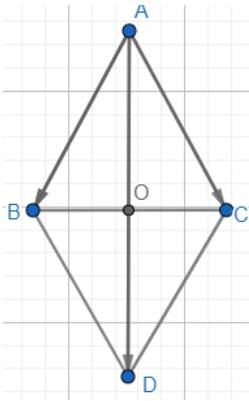
Áp dụng quy tắc hình bình hành vào ABDC ta có:
\(\overrightarrow {AB} + \overrightarrow {AC} = \overrightarrow {AD} \Rightarrow \left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = \left| {\overrightarrow {AD} } \right| = AD\)
Gọi O là giao điểm của AD và BC, ta có:
\(AO = \sqrt {A{B^2} - B{O^2}} = \sqrt {A{B^2} - {{\left( {\frac{1}{2}BC} \right)}^2}} = \sqrt {{a^2} - {{\left( {\frac{a}{2}} \right)}^2}} = \frac{{a\sqrt 3 }}{2}\)
\(AD = 2AO = a\sqrt 3 \Rightarrow \left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = a\sqrt 3 \)
Vậy độ dài vectơ \(\overrightarrow {AB} + \overrightarrow {AC} \) là \(a\sqrt 3 \)