Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi O là trung điểm của AM
BM=BC/2=a/2
\(\Leftrightarrow AM=\dfrac{a\sqrt{3}}{2}\)
\(\Leftrightarrow MO=\dfrac{a\sqrt{3}}{4}\)
Xét ΔOMB vuông tại M có
\(BO^2=OM^2+BM^2\)
\(=a^2\cdot\dfrac{3}{16}+a^2\cdot\dfrac{1}{4}=a^2\cdot\dfrac{7}{16}\)
\(\Leftrightarrow BO=\dfrac{a\sqrt{7}}{4}\)
Xét ΔBMA có BO là đường trung tuyến
nên \(\overrightarrow{BM}+\overrightarrow{BA}=2\cdot\overrightarrow{BO}\)
\(\Leftrightarrow\left|\overrightarrow{BM}+\overrightarrow{BA}\right|=\dfrac{a\sqrt{7}}{2}\)

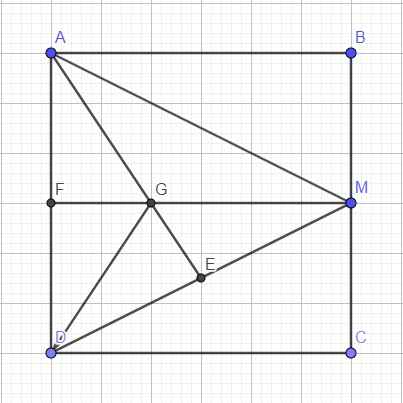
\(\left\{{}\begin{matrix}AM=\sqrt{AB^2+BM^2}=3\sqrt{5}\\DM=\sqrt{CD^2+CM^2}=3\sqrt{5}\end{matrix}\right.\) \(\Rightarrow\) tam giác ADM cân tại M
Gọi F là trung điểm AD \(\Rightarrow ABMF\) là hình chữ nhật \(\Rightarrow MF=AB=6\)
Theo tính chất trọng tâm: \(GF=\dfrac{1}{3}MF=2\)
\(DF=\dfrac{1}{2}AD=3\)
Đặt \(T=\left|\overrightarrow{GD}\right|=\left|\overrightarrow{GF}+\overrightarrow{FD}\right|\)
\(\Rightarrow T^2=GF^2+FD^2+2\overrightarrow{GF}.\overrightarrow{DF}=GF^2+DF^2=2^2+3^2=13\)
\(\Rightarrow\left|\overrightarrow{GD}\right|=\sqrt{13}\)

E là trung điểmcủa BC
=>EB=EC=a/2
\(AE=\sqrt{AB^2+BE^2}=\dfrac{a\sqrt{5}}{2}\)
Xét ΔABE vuông tại B có \(\left\{{}\begin{matrix}cosBAE=\dfrac{AB}{AE}=\dfrac{a}{\dfrac{a\sqrt{5}}{2}}=\dfrac{2}{\sqrt{5}}\\sinBAE=\dfrac{BE}{AE}=\dfrac{0.5a}{\dfrac{a\sqrt{5}}{2}}=\dfrac{1}{\sqrt{5}}\end{matrix}\right.\)
=>\(cosDAF=cosBEA=sinBAE=\dfrac{1}{\sqrt{5}}\)
\(AF=\dfrac{AE}{2}=\dfrac{a\sqrt{5}}{4}\)
Xét ΔADF có \(cosDAF=\dfrac{AD^2+AF^2-DF^2}{2\cdot AD\cdot AF}\)
=>\(\dfrac{a^2+a^2\cdot\dfrac{5}{16}-DF^2}{2\cdot\dfrac{a\sqrt{5}}{4}\cdot a}=\dfrac{1}{\sqrt{5}}\)
=>\(\dfrac{\dfrac{21}{16}a^2-DF^2}{\dfrac{a^2\sqrt{5}}{2}}=\dfrac{1}{\sqrt{5}}\)
=>\(\dfrac{21}{16}a^2-DF^2=\dfrac{a^2}{2}\)
=>\(DF^2=\dfrac{13}{16}a^2\)
=>\(DF=\dfrac{a\sqrt{13}}{4}\)
I là trung điểm BC \(\Rightarrow\overrightarrow{BI}=\dfrac{1}{2}\overrightarrow{BC}=\dfrac{1}{2}\overrightarrow{AD}\Rightarrow2\overrightarrow{BI}=\overrightarrow{AD}\)
\(\overrightarrow{u}=2\left(\overrightarrow{AB}+\overrightarrow{BI}\right)-3\overrightarrow{AD}=2\overrightarrow{AB}+2\overrightarrow{BI}-3\overrightarrow{AD}=2\overrightarrow{AB}-2\overrightarrow{AD}=2\left(\overrightarrow{AB}+\overrightarrow{DA}\right)=2\overrightarrow{DB}\)
\(\Rightarrow\left|\overrightarrow{u}\right|=2\left|\overrightarrow{DB}\right|=2DB=2a\sqrt{2}\)
em thưa thầy em chưa hiểu đoạn 2AB+2BI-3AD tại sao ra 2AB-2AD ạ