Cho xyz=2019. Tính giá trị biểu thức \(A=\dfrac{2019x}{xy+2019x+2019}+\dfrac{y}{yz+y+2019}+\dfrac{z}{xz+z+1}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
4 tháng 3 2020
\(P=\frac{2019xz}{xyz+2019xz+2019z}+\frac{y}{yz+y+xyz}+\frac{z}{xz+z+1}\)
\(=\frac{2019xz}{2019+2019xz+2019z}+\frac{y}{y\left(xz+z+1\right)}+\frac{z}{xz+z+1}\)
\(\frac{xz}{xz+z+1}+\frac{1}{xz+z+1}+\frac{z}{xz+z+1}=1\)
22 tháng 5 2022
\(A=\dfrac{1}{xy+x+1}+\dfrac{1}{yz+y+1}+\dfrac{1}{xz+z+1}\)
\(A=\dfrac{1}{xy+x+xyz}+\dfrac{1}{yz+y+1}+\dfrac{1}{xz+z+1}\)
\(A=\dfrac{1}{x\left(y+1+yz\right)}+\dfrac{1}{yz+y+1}+\dfrac{1}{xz+z+1}\)
\(A=\dfrac{xyz}{x\left(y+1+yz\right)}+\dfrac{1}{yz+y+1}+\dfrac{1}{xz+z+1}\)
\(A=\dfrac{yz}{y+1+yz}+\dfrac{1}{y+yz+1}+\dfrac{1}{xz+z+1}\)
\(A=\dfrac{yz+1}{y+1+yz}+\dfrac{1}{xz+z+1}\)
\(A=\dfrac{yz+xyz}{y+xyz+yz}+\dfrac{1}{xz+z+1}\)
\(A=\dfrac{y\left(z+xz\right)}{y\left(1+xz+z\right)}+\dfrac{1}{xz+z+1}\)
\(A=\dfrac{z+xz+1}{xz+z+1}\)
\(A=1\)
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 8 2021
\(T\ge\dfrac{\left(x+y+z\right)^2}{x+y+z+\sqrt{xy}+\sqrt{yz}+\sqrt{zx}}\ge\dfrac{\left(x+y+z\right)^2}{x+y+z+x+y+z}=\dfrac{x+y+z}{2}\ge\dfrac{2019}{2}\)
7 tháng 8 2021
áp dụng BĐT:\(\dfrac{a^2}{x}+\dfrac{b^2}{y}+\dfrac{c^2}{z}\) với a,b,c,x,y,z là số dương
ta có BĐT Bunhiacopxki cho 3 bộ số:\(\left(\dfrac{a}{\sqrt{x}};\sqrt{x}\right);\left(\dfrac{b}{\sqrt{y}};\sqrt{y}\right);\left(\dfrac{c}{\sqrt{z}};\sqrt{z}\right)\)
ta có :
\(\dfrac{a^2}{x}+\dfrac{b^2}{y}+\dfrac{c^2}{z}\left(x+y+z\right)\)\(=\left[\left(\dfrac{a}{\sqrt{x}}\right)^2+\left(\dfrac{b}{\sqrt{y}}\right)^2+\left(\dfrac{c}{\sqrt{z}}\right)^2\right]\).\(\left[\left(\sqrt{x}\right)^2+\left(\sqrt{y}\right)^2+\left(\sqrt{z}\right)^2\right]\)\(\ge\left(\dfrac{a}{\sqrt{x}}.\sqrt{x}+\dfrac{b}{\sqrt{y}}.\sqrt{y}+\dfrac{c}{\sqrt{z}}.\sqrt{z}\right)^2=\left(a+b+c\right)^2\)
lúc đó ta có :\(\dfrac{a^2}{x}+\dfrac{b^2}{y}+\dfrac{c^2}{z}\ge\dfrac{\left(a+b+c\right)^2}{x+y+z}\)
ta có \(T=\dfrac{x^2}{x+\sqrt{yz}}+\dfrac{y^2}{y+\sqrt{zx}}+\dfrac{z^2}{z+\sqrt{xy}}\)\(\ge\dfrac{\left(x+y+z\right)^2}{x+\sqrt{yz}+y+\sqrt{zx}+z+\sqrt{xy}}\) mà ta có :
\(\sqrt{yz}+\sqrt{zx}+\sqrt{xy}\)\(\le\dfrac{x+y}{2}+\dfrac{x+z}{2}+\dfrac{z+y}{2}\)\(\Rightarrow\sqrt{yz}+\sqrt{zx}+\sqrt{xy}\le x+y+z\)
\(\Rightarrow T=\dfrac{2019}{2}\Leftrightarrow x=y=z=673\)
vậy \(\text{MinT}=\dfrac{2019}{2}\) khi và chỉ khi x=y=z=673
18 tháng 6 2018
Áp dụng BĐT Cauchy cho các số dương , ta có :
\(\dfrac{xy}{z}+\dfrac{yz}{x}\) ≥ \(2\sqrt{\dfrac{xy}{z}.\dfrac{yz}{x}}=2\sqrt{y^2}=2y\left(1\right)\)
\(\dfrac{yz}{x}+\dfrac{xz}{y}\) ≥ \(2\sqrt{\dfrac{yz}{x}.\dfrac{xz}{y}}=2\sqrt{z^2}=2z\left(2\right)\)
\(\dfrac{xy}{z}+\dfrac{xz}{y}\) ≥ \(2\sqrt{\dfrac{xy}{z}.\dfrac{xz}{y}}=2\sqrt{x^2}=2x\left(3\right)\)
Cộng từng vế của ( 1 ; 2 ; 3) , ta được :
\(2\left(\dfrac{xy}{z}+\dfrac{yz}{x}+\dfrac{xz}{y}\right)\) ≥ \(2\left(x+y+z\right)\)
⇔ \(\dfrac{xy}{z}+\dfrac{yz}{x}+\dfrac{xz}{y}\) ≥ \(x+y+z=2019\)
⇒ \(P_{Min}=2019\) ⇔ \(x=y=z=673\)
DT
0
10 tháng 11 2021
\(\dfrac{1}{\left(x-y\right)\left(z^2+yz-x^2-xz\right)}=\dfrac{1}{\left(x-y\right)\left[\left(z-x\right)\left(z+x\right)+y\left(z-x\right)\right]}=\dfrac{1}{\left(z-x\right)\left(x-y\right)\left(x+y+z\right)}\)
Tương tự: \(\dfrac{1}{\left(y-z\right)\left(x^2+xz-y^2-yz\right)}=\dfrac{1}{\left(y-z\right)\left(x-y\right)\left(x+y+z\right)}\)
\(\dfrac{1}{\left(z-x\right)\left(y^2+xy-z^2-xz\right)}=\dfrac{1}{\left(z-x\right)\left(y-z\right)\left(x+y+z\right)}\)
\(\Rightarrow M=\dfrac{y-z-z+x-x+y}{\left(x-y\right)\left(y-z\right)\left(z-x\right)\left(x+y+z\right)}\\ M=\dfrac{2}{\left(x-y\right)\left(z-x\right)\left(x+y+z\right)}\)
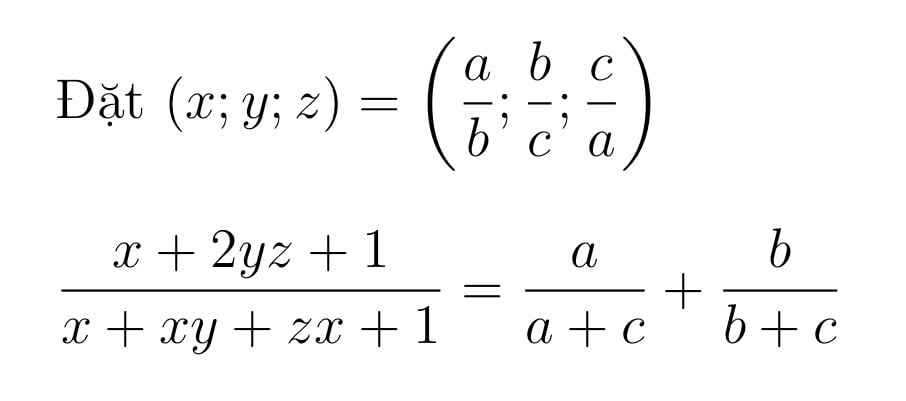
\(A=\dfrac{xyz.x}{xy+xyz.x+xyz}+\dfrac{y}{yz+y+2019}+\dfrac{yz}{xyz+yz+y}\)
\(=\dfrac{xz}{1+xz+z}+\dfrac{y}{yz+y+2019}+\dfrac{yz}{yz+y+2019}\)
\(=\dfrac{xyz}{y+xyz+yz}+\dfrac{y}{yz+y+2019}+\dfrac{yz}{yz+y+2019}\)
\(=\dfrac{2019}{y+2019+yz}+\dfrac{y}{yz+y+2019}+\dfrac{yz}{yz+y+2019}\)
\(=\dfrac{yz+y+2019}{yz+y+2019}=1\)