Một quân vua được đặt ở vị trí e4. Mỗi bước di chuyển, quân vua được chuyển sang một ô khác chung cạnh hoặc chung đỉnh với ô đang đứng. Bạn An di chuyển quân vua ngẫu nhiên 3 bước. Tính xác suất sau 3 bước quân vua trở về vị trí ban đầu
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
10 tháng 12 2018
Đáp án D
Phương pháp :
Quân vua được di chuyển sang một ô khác chung cạnh hoặc chung đỉnh với ô đang đứng => | Ω |
Gọi A là biến cố : « Quân vua sau 3 bước trở về đúng vị trí ban đầu » . Tính |A| .
Cách giải :
Quân vua được di chuyển sang một ô khác chung cạnh hoặc chung đỉnh với ô đang đứng => | Ω | = 8 3 .
Gọi A là biến cố : « Quân vua sau 3 bước trở về đúng vị trí ban đầu »
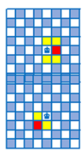
TH1: Quân vua di chuyển bước thứ nhất sang ô đen liền kề (được tô màu đỏ) có 4
cách.
Bước đi thứ 2 quân vua di chuyển sang các ô được tô màu vàng có 4 cách.
Bước đi thứ 3 quay về vị trí ban đầu có 1 cách.
Vậy TH này có 4.4 = 16 cách.
TH2: Quân vua di chuyển bước thứ nhất sang các ô trắng liền kề (được tô màu đỏ) có
4 cách.
Bước đi thứ 2 quân vua di chuyển sang các ô được tô màu vàng có 2 cách.
Bước đi thứ 3 quay về vị trí ban đầu có 1 cách.
Vậy TH này có 4.2 = 8 cách
CM
29 tháng 8 2018
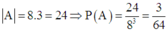
Chọn A
Không gian mẫu là 8 3
Có hai trường hợp
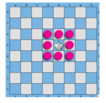
+ Trường hợp 1: Bước 1 đi 4 ô góc thì bước 2 có 2 cách đi, bước 3 có 1 cách đi
+ Trường hợp 2: Bước 1 đi 4 ô còn lại thì bước 2 có 4 cách đi, bước 3 có 1 cách đi
Vậy tât cả có 4.2 + 4.4 = 24
Suy ra xác suất để sau 3 bước đi quân vua trở về ô ban đầu là: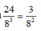 
CM
19 tháng 12 2019
Chọn A
Mỗi lần di chuyển, quân cờ chỉ có thể di chuyển một trong bốn cách sau: lên trên 1 ô (U), xuống dưới 1 ô (D), sang phải 1 ô (R), sang trái 1 ô (L). Quân cờ di chuyển bốn lần sẽ có 4 4 = 256 cách.
⇒ n ( Ω ) = 256 cách
Gọi A là biến cố quân cờ không trở về đúng vị trí ban đầu sau bốn lần di chuyển.
=> A ¯ là biến cố quân cờ trở về đúng vị trí ban đầu sau bốn lần đi chuyển.
Để quân cờ trở về đúng vị trí ban đầu sau bốn lần đi chuyển thì phải thực hiện 1 trong 3 trường hợp sau:
Trường hợp 1: Có một U, một D, một R, một L.
Xếp cách thực hiện U, D, R, L theo thứ tự có 4! = 24 cách.
Trường hợp 2: Có hai U, hai D.
Xếp cách thực hiện hai U, hai D theo thứ tự có 
cách.
Trường hợp 3: Có hai R, hai L.
Xếp cách thực hiện hai R, hai L theo thứ tự có 
cách.
7 tháng 12 2021
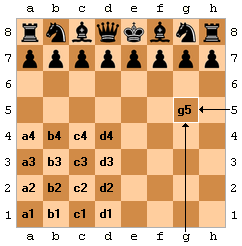
Theo hình ta thấy quãng đường quân hậu di chuyển là 1 tam giác vuông cân có cạnh góc vuông là cạnh chung với cạnh của bàn cờ
Ta có cạnh bàn cờ là \(\sqrt{40}=2\sqrt{10}\left(cm\right)\)
Áp dụng PTG, cạnh huyền của tam giác vuông cân là \(\sqrt{\left(2\sqrt{10}\right)^2+\left(2\sqrt{10}\right)^2}=4\sqrt{10}\left(cm\right)\)
Vậy tổng quãng đường quân hậu di chuyển là \(2\sqrt{10}\cdot2+4\sqrt{10}=8\sqrt{10}\left(cm\right)\)