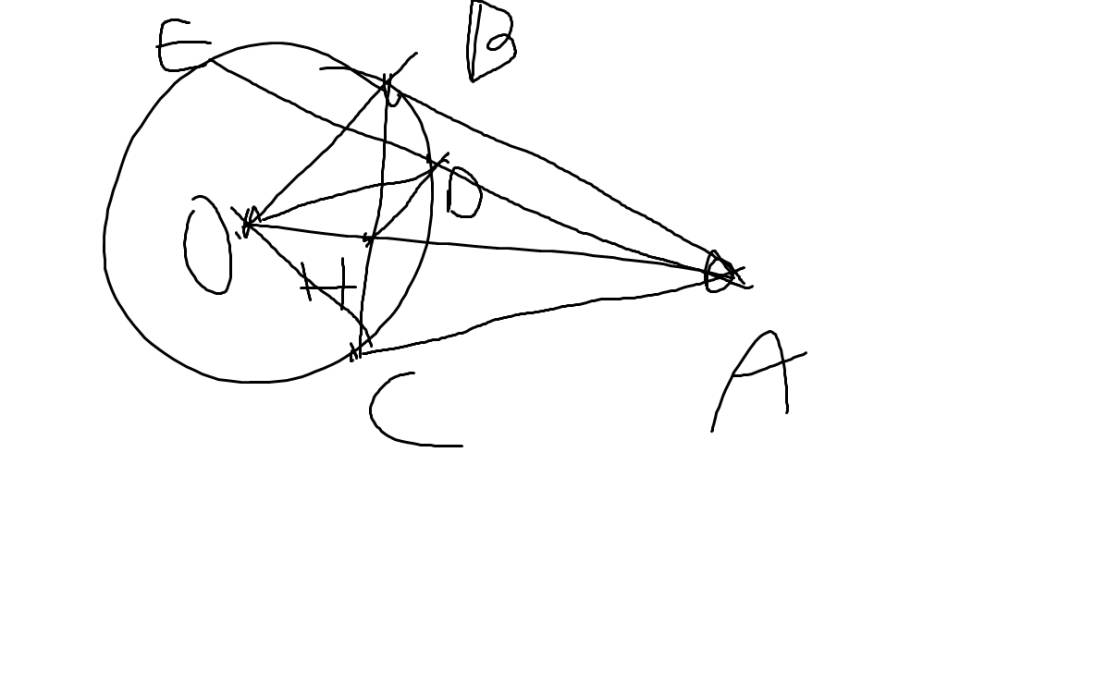
Bài 1: Từ điểm A ở bên ngoài đường tròn (O), kẻ hai tiếp tuyến AB, AC đến đường tròn (O) (B,C là hai tiếp điểm). Kẻ cát tuyến ADE vs đường tròn (O) (D nằm giữa A và E).a) cm: A,B,O,C cùng thuộc một đường tròn.b) cm: OA vuông BC tại H và OD2 = OH.OA. Từ đó suy ra tam giác OHD đồng dạng vs tam giác ODA.c) cm: BC trùng với tia phân giác của góc DHE.d) Từ D kẻ đường thẳng song song với BE, đường...
Đọc tiếp
Bài 1: Từ điểm A ở bên ngoài đường tròn (O), kẻ hai tiếp tuyến AB, AC đến đường tròn (O) (B,C là hai tiếp điểm). Kẻ cát tuyến ADE vs đường tròn (O) (D nằm giữa A và E).
a) cm: A,B,O,C cùng thuộc một đường tròn.
b) cm: OA vuông BC tại H và OD2 = OH.OA. Từ đó suy ra tam giác OHD đồng dạng vs tam giác ODA.
c) cm: BC trùng với tia phân giác của góc DHE.
d) Từ D kẻ đường thẳng song song với BE, đường thẳng này cắt AB, AC lần lượt tại M và N. cm: D là trung điểm MN.
Bài 2: Cho đường tròn tâm O bán kính R, dây BC khác đường kính. Hai tiếp tuyến của đường tròn (O,R) tại B và tại C cắt nhau tại A. Kẻ đường kính CD, kẻ BH vuông góc vs CD tại H.
a) cm: A,B,O,C cùng thuoojcj một đường tròn. Xác định tâm và bán kính của đường tròn đó.
b) cm: AO vuông góc vs BC. Cho biết R=15cm, BC=24cm. Tính AB, OA.
c) cm: BC là tia phân giác của góc ABH.
d) Gọi I là giao điểm của AD và BH, E là giao điểm của BD và AC. cm: IH=IB.

a: Xét tứ giác ABOC có \(\widehat{OBA}+\widehat{OCA}=90^0+90^0=180^0\)
nên ABOC là tứ giác nội tiếp
=>O,B,A,C cùng thuộc một đường tròn
b: Xét (O) có
AB,AC là các tiếp tuyến
Do đó: AB=AC
=>A nằm trên đường trung trực của BC(1)
Ta có OB=OC
=>O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra OA là đường trung trực của BC
=>OA\(\perp\)BC tại H và H là trung điểm của BC
Xét ΔOBA vuông tại B có BH là đường cao
nên \(OH\cdot OA=OB^2\)
mà OB=OD(=R)
nên \(OD^2=OH\cdot OA\)
=>\(\dfrac{OD}{OH}=\dfrac{OA}{OD}\)
Xét ΔODA và ΔOHD có
\(\dfrac{OD}{OH}=\dfrac{OA}{OD}\)
\(\widehat{DOA}\) chung
Do đó: ΔODA đồng dạng với ΔOHD