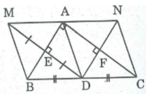
cho tam giác ABC vuông tại A , D là trung của BC. kẻ DE vuông góc với AC . Gọi M là điểm đối xứng với D qua AB I là giao điểm của DM và AB
a, cm tứ giác AIDE là hình chữ nhật
b, tứ giác ADBM là hình gì vì sao
c, cm MD=AC
d, để tứ giác AIDE là hình vuông thì ABC cần điều kiện gì



mong mọi người giúp hộ mình