Hai bức tường cách nhau 4m, ở 1 trong 2 bức tường người ta đặt một bóng đèn nhỏ và đứng giữa 2 bức tường này có đặt một vật cản sáng hình tròn đường kính 60cm.
a) Tìm đường kính bóng của vật cản sáng trên tường
b) Nếu ở giữa vật cản có một lỗ tròn đường kính 10cm thì diện tích bóng tối là bao nhiêu?

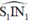 bằng góc phản xạ
bằng góc phản xạ 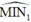 nghĩa là:
nghĩa là: 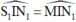 . Ta xác định được tia tới S
. Ta xác định được tia tới S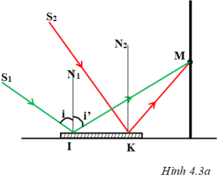


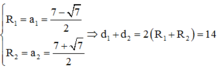


Tóm tắt:
D = 4 m; vật cản có d = 60cm. SO = 2 m.
a) Tìm dtối
b) Giữa vật cản có lỗ dlỗ = 10 cm thì Stối = ?
Bài giải:
a) Ta có hình vẽ:
Vì vật sáng đặt giữa hai bức tường nên SO = 2m. Bán kính của vùng tối là A’I.
Ta có tam giác ∆ SAO ~ ∆ SA’I nên ta có:
S O S I = A O A ' I ⇒ A ' I = A O . S I S O = 30. 4 2 = 60 c m
Vậy đường kính vùng tối là dtối = 2.A’I = 2.60 = 120 cm.
b)
Khi trên tấm bìa có 1 lỗ tròn đường kính 10 cm, tức là bán kính lỗ tròn CO = 5 cm.
Ta có tam giác ∆ SCO ~ ∆ SC’I. Vậy ta có:
S O S I = C O C ' O ⇒ C ' O = C O . S I S O = 5. 4 2 = 10 c m
Vậy bóng tối trên tường là 1 hình tròn bán kính R = 30 cm và có 1 hình tròn sáng đồng tâm có bán kính r = 10cm.
Diện tích vùng bóng tối trên màn là S = π.R2 – π.r2 = π.(302 - 102) = 2512 cm2.