Hình chóp tam giác đều S . A B C có cạnh đáy bằng 3 a , cạnh bên bằng 3 a . Tính khoảng cách h từ đỉnh S tới mặt phẳng đáy A B C .
A. h = a
h = a 6 B.
C. h = 3 2 a
D. h = a 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

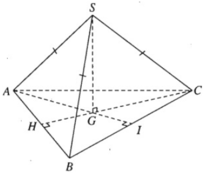
a) SG là trục đường tròn ngoại tiếp tam giác đều ABC nên SG ⊥ (ABC). Ta có
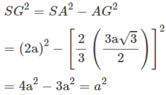
Vậy khoảng cách từ S tới mặt phẳng (ABC) là độ dài của đoạn SG = a
Ta có CG ⊥ AB tại H. Vì GH là đoạn vuông góc chung của AB và SG, do đó
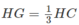
mà 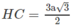
nên 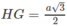

Đáp án C
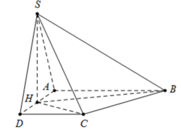
Tam giác SAD đều cạnh 2 a ⇒ S H = a 3 ⇒ H C − 2 a 3 .
Kẻ BK vuông góc H C ⇒ B K ⊥ S H C ⇒ B K − 2 a 6
Diện tích tam giác BHC là S Δ B H C = 1 2 B K . H C = 6 a 2 2
Mà S A B C D = S Δ H A B + S Δ H C D + S Δ H B C = 1 2 S A B C D + S Δ H B C ⇒ S A B C D = 2 x S Δ H B C = 12 a 2 2
V S . A B C D = 1 3 . S H . S Δ H B C = 1 3 . a 3 .12 a 2 2 = 4 6 a 3

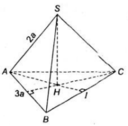
Gọi H là tâm của tam giác ABC ( khi đó H là trọng tâm, trực tâm của tam giác ABC).
Do hình chóp S.ABC là hình chóp tam giác đều nên SH ⊥ (ABC)

Vậy khoảng cách từ S đến (ABC ) là a.

Gọi H là tâm của tam giác ABC ( khi đó H là trọng tâm, trực tâm của tam giác ABC).
Do hình chóp S.ABC là hình chóp tam giác đều nên SH ⊥ (ABC)
\(AN=\sqrt{AB^2-BN^2}\) \(=\) \(\sqrt{\left(3a\right)^2-\left(\dfrac{3a}{2}\right)^2}\) \(=\) \(\dfrac{3a\sqrt{3}}{2}\)
Vậy khoảng cách từ S đến (ABC ) là a.

Đáp án B
Gọi H là trung điểm của AD, vì ΔASD cân ở S nên SH ⊥ AD.
Vì (SAD)⊥(ABCD) nên SH ⊥ (ABCD). Kẻ HI ⊥ SD.
Vì DC ⊥ AD, DC ⊥ SH nên DC ⊥ (SAD). Do đó DC ⊥ HI.
Kết hợp với HI ⊥ SD, suy ra HI ⊥ (SDC).
Vì AB // (SDC) nên d(B; (SDC)) = d(A; (SDC)) = 2HI
Ta có
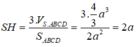
Ta lại có


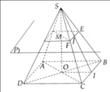
a) Gọi O là tâm của đáy ABCD, M là giao điểm của SO và mặt phẳng (P). Ta có: OM = 2(cm).
Ta tính được O B = 2 2 c m rồi suy ra SO = 5 (cm)
Từ đó chiều cao cần tìm là: SM = SO - OM 3 (cm)
b) Gọi I là trung điểm của BC. E, F, J lần lượt là giao điểm của SB, SC, SI với mặt phẳng (p).
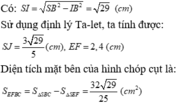
Đáp án là B
Gọi H là tâm của tam giác đều A B C ⇒ S H ⊥ A B C .
Gọi M là trung điểm của B C .
Ta có A M = 3 a 3 2 ; A H = 2 3 A M = a 3 .
Xét tam giác S A H : S H = S A 2 − A H 2 = a 6 . Vậy h = d S ; A B C = S H = a 6 .