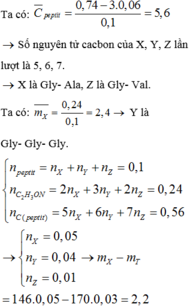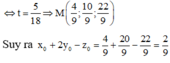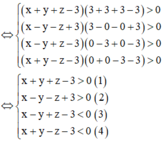Cho X, Y, Z (MX<MY<MZ) là ba peptit mạch hở, được tạo từ Gly, Ala, Val; T là este mạch hở, được tạo từ một axit cacbonxylic và một ancol. Thủy phân hoàn toàn 21,7 gam hỗn hợp E gồm X, Y, Z, T cần vừa đủ 0,3 lít dung dịch KOH 1M, thu được 1,86 gam etylen glicol và hỗn hợp muối M. Đốt cháy hoàn toàn M cần vừa đủ 0,84 mol O2, thu được N2, K2CO3, H2O và 25,96 gam CO2. Biết số nguyên tử cacbon trong phân tử X, Y, Z là ba số tự nhiên liên tiếp. Hiệu khối lượng của X và T trong 21,7 gam E là
A. 1.87 gam
B. 2.20 gam
C. 1,66 gam
D. 3,78 gam