Qua trọng tâm G của tam giác ABC ,kẻ đường thẳng song song với AC ,cắt và BC lần lượt tại M và N .tính độ dài MN ,biết AM+NC=16cm ;chu vi của ABC bằng 75cm
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
H9
HT.Phong (9A5)
CTVHS
16 tháng 1
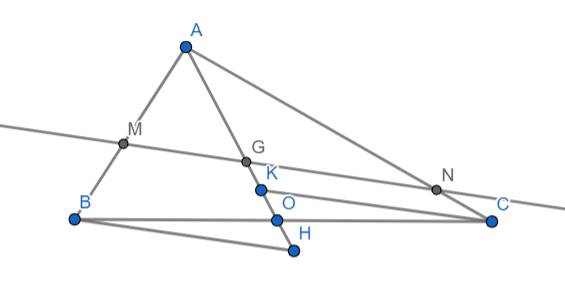
Xét 2 tam giác AMG và ABH ta có:
\(\widehat{BAH}\) chung
\(\widehat{AMG}=\widehat{ABH}\) (cặp góc đồng vị do BH//MG)
\(\Rightarrow\Delta AMG\sim\Delta ABH\left(g.g\right)\)
\(\Rightarrow\dfrac{AB}{AM}=\dfrac{AH}{AG}\) (1)
Xét 2 tam giác ANG và ACK có:
\(\widehat{CAK}\) chung
\(\widehat{ANG}=\widehat{ACK}\) (cặp góc đồng vị do CK//GN)
\(\Rightarrow\Delta ANG\sim\Delta ACK\left(g.g\right)\)
\(\Rightarrow\dfrac{AC}{AN}=\dfrac{AK}{AG}\) (2)
Xét hai tam giác BOH và COK ta có:
\(\widehat{BOH}=\widehat{COK}\) (đối đỉnh)
\(BO=CO\) (AO là đường trung tuyến nên O là trung điểm của BC)
\(\widehat{HBO}=\widehat{KCO}\) (so le trong vì BH//MN và CK//MN ⇒ BH//CK)
\(\Rightarrow\Delta BOH=\Delta COK\left(g.c.g\right)\)
\(\Rightarrow HO=OK\) (hai cạnh t.ứng)
\(\Rightarrow HK=2HO\)
Ta lấy (1) + (2) \(\Rightarrow\dfrac{AB}{AM}+\dfrac{AC}{AN}=\dfrac{AH+AK}{AG}=\dfrac{AH+AH+HK}{AG}=\dfrac{2AH+HK}{AG}\)
\(=\dfrac{2AH+2HO}{AG}=\dfrac{2\left(AH+HO\right)}{AG}=\dfrac{2AO}{AG}\)
Mà G là trọng tâm của tam giác ABC \(\Rightarrow AO=\dfrac{3}{2}AG\)
\(\Rightarrow\dfrac{AB}{AM}+\dfrac{AC}{AN}=\dfrac{2\cdot\dfrac{3}{2}AG}{AG}=2\cdot\dfrac{3}{2}=3\left(đpcm\right)\)
12 tháng 3 2021
Dễ thấy H là trực tâm của tam giác ABC.
a) Bỏ qua
b) Gọi T là trung điểm của HC.
Ta có NT là đường trung bình của tam giác AHC nên NT // AH. Suy ra NT // OM.
TM là đường trung bình của tam giác BHC nên MT // BH. Suy ra MT // ON.
Từ đó tứ giác NTMO là hình bình hành nên OM = NT = \(\dfrac{AH}{2}\).
Xét \(\Delta AHG\) và \(\Delta MOG\) có: \(\widehat{HAG}=\widehat{OMG}\) (so le trong, AH // OM) và \(\dfrac{AH}{MO}=\dfrac{AG}{MG}\left(=2\right)\).
Do đó \(\Delta AHG\sim\Delta MOG\left(c.g.c\right)\).
c) Do \(\Delta AHG\sim\Delta MOG\left(c.g.c\right)\) nên \(\widehat{AGH}=\widehat{MGO}\), do đó H, G, O thẳng hàng.
7 tháng 4 2021
a) Xét ΔABC có
MN//BC(gt)
Do đó: \(\dfrac{AM}{MB}=\dfrac{AN}{NC}\)(Định lí Ta lét)
Suy ra: \(\dfrac{6}{4}=\dfrac{8}{NC}\)
hay \(NC=\dfrac{16}{3}cm\)
Ta có: AM+MB=AB(M nằm giữa A và B)
nên AB=6+4=10(cm)
Ta có: AN+NC=AC(N nằm giữa A và C)
nên \(AC=8+\dfrac{16}{3}=\dfrac{40}{3}cm\)
Áp dụng định lí Pytago vào ΔBAC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=10^2+\left(\dfrac{40}{3}\right)^2=\dfrac{2500}{9}\)
hay \(BC=\dfrac{50}{3}cm\)
Xét ΔABC có
MN//BC(gt)
nên \(\dfrac{MN}{BC}=\dfrac{AM}{AB}\)(Hệ quả của Định lí Ta lét)
\(\Leftrightarrow\dfrac{MN}{\dfrac{50}{3}}=\dfrac{6}{10}\)
\(\Leftrightarrow MN=\dfrac{6\cdot\dfrac{50}{3}}{10}=\dfrac{100}{10}=10cm\)
Vậy: MN=10cm; \(NC=\dfrac{16}{3}cm\); \(BC=\dfrac{50}{3}cm\)
T/g BMN đồng dạng vs t/g BAC theo tỉ số 2/3 => C(BMN) = 2/3 C(BAC) = 50cm
\(\frac{MB}{AB}=\frac{2}{3}\Rightarrow\frac{MB}{AB-MB}=\frac{MB}{AM}=\frac{2}{3-2}=2\Rightarrow MB=2AM\)
tương tự, BN=2NC
MN = C(BMN) - BM - BN = 50 - 2(AM+NC) = 18cm