Cho hình hộp đứng A B C D . A ' B ' C ' D ' . Xét tất cả các hình bình hành có đỉnh là đỉnh của hình hộp đó. Hỏi có bao nhiêu hình bình hành mà mặt phẳng chứa nó vuông góc với mặt phẳng đáy (ABCD)?
A. 4
B. 6
C. 8
D. 10
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tương tự 2A
a) (i) Có 8 đỉnh, 12 cạnh và 6 mặt.
(ii) Hình lăng trụ đứng ABDC.A'B'D'C' không là hình hộp chữ nhật vì các đáy không phải là hình chữ nhật.
b) (BCC'B') ^ (ABDC)

a) HÌNH HỘP CHỮ NHẬT CÓ 6 MẶT , 12 CẠNH, 8 ĐỈNH .
b) TẤT CẢ CÁC MẶT CỦA HÌNH HỘP CHỮ NHẬT ĐỀU LÀ HÌNH CHỮ NHẬT .
c) HÌNH LẬP PHƯƠNG CÓ 6 MẶT ,12 CẠNH , 8 ĐỈNH .
d) TẤT CẢ CÁC MẶT CỦA HÌNH LẬP PHƯƠNG ĐỀU CÓ ĐỘ DÀI GIỐNG NHAU .
e) TẤT CẢ CÁC MẶT CỦA HÌNH LẬP PHƯƠNG ĐỀU LÀ HÌNH VUÔNG.
HẾT ................................................ .

Đáp án B
Mặt phẳng cách đều 5 điểm là mặt phẳng mà khoảng cách từ 5 điểm đó đến mặt phẳng là bằng nhau.
Có 5 mặt phẳng thỏa mãn là:
+ Mặt phẳng đi qua trung điểm của AB,CD và song song với SBC .
+ Mặt phẳng đi qua trung điểm của AB,CD và song song với SAD .
+ Mặt phẳng đi qua trung điểm của AD,BC và song song với SAB .
+ Mặt phẳng đi qua trung điểm của AD,BC và song song với SCD .
+ Mặt phẳng đi qua trung điểm của SA,SB,SC,SD.

Đáp án D
Tồn tại 5 mặt phẳng thỏa mãn đề bài là:
- Mp đi qua trung điểm AD,BC,SC,SD
- Mp đi qua trung điểm CD,AB,SC,SB
- Mp đi qua trung điểm AD,BC,SB,SA
- Mp đi qua trung điểm CD,AB,SA,SD
- Mp đi qua trung điểm SA,SB,SC,SD

Đáp án B
Phương pháp:
Gọi các trung điểm của các cạnh bên và các cạnh đáy.
Tìm các mặt phẳng cách đều 5 điểm S, A, B, C, D.
Cách giải:
Gọi E; F; G; H lần lượt là trung điểm của SA, SB, SC, SD và M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA .
Ta có thể tìm được các mặt phẳng cách đều 5 điểm S, A, B, C, D là (EFGH); (EFNQ); (GHQN); (FGPM); (EHPM)
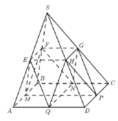

Đáp án D
Tồn tại 5 mặt phẳng thỏa mãn đề bài là:
- Mp đi qua trung điểm AD,BC,SC,SD
- Mp đi qua trung điểm CD,AB,SC,SB
- Mp đi qua trung điểm AD,BC,SB,SA
- Mp đi qua trung điểm CD,AB,SA,SD
- Mp đi qua trung điểm SA,SB,SC,SD

1, Gọi tọa độ điểm D(x;y)
Ta có:\(\overrightarrow{AB}\left(8;1\right)\)
\(\overrightarrow{DC}\left(1-x;5-y\right)\)
Tứ giác ABCD là hình bình hành khi
\(\overrightarrow{AB}=\overrightarrow{DC}\)
\(\Leftrightarrow1-x=8;5-y=1\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=-7\\y=4\end{matrix}\right.\)
Vậy tọa độ điểm D(-7;4)
Đáp án B
Cách giải:
Có 6 hình bình hành thỏa mãn yêu cầu:
A B B ' A ' ; B C C ' B ' ; C DD ' C ' ; A D D ' A ' ; A C C ' A ' ; B DD ' B '