Cho tam giác ABC có phương trình canh BC: 4x – y + 3 = 0 và hai đường phân giác trong của góc B, góc C lần lượt có phương trình x – 2y + 1 = 0; x + y + 3 = 0. Viết phương trình các cạnh còn lại của tam giác ABC.
mn giúp mình câu này với ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
24 tháng 4 2020
Gọi D là giao điểm của hai đường phân giác trong góc B và góc C
+) Trên BC lấy điểm M sao cho: AM vuông BD tại H
=> Đường thẳng AM \(\perp\)BH => AM có dạng: 2x + y + a = 0
mà A ( 2; -1) \(\in\)AM => 2.2 + ( -1) + a = 0 <=> a = -3
=> phương trình đt: AM : 2x + y - 3 = 0
H là giao của AM và BD => Tọa độ điểm H là nghiệm hệ: \(\hept{\begin{cases}x-2y+1=0\\2x+y-3=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=1\\y=1\end{cases}}\)=> H ( 1; 1)
Lại có: BH vừa là đường cao vừa là đường phân giác \(\Delta\)ABM => \(\Delta\)ABM cân => H là trung điểm AM
=> \(\hept{\begin{cases}x_M=2x_H-x_A=2.1-2=0\\y_M=2y_H-y_B=2.1-\left(-1\right)=3\end{cases}}\)=> M ( 0; 3 )
+) Trên BC lấy lấy điêm N sao cho AN vuông CD tại K
Làm tương tự như trên ta có:
AN có dạng: x - y + b = 0 mà A thuộc AN => 2 + 1 + b = 0 => b = - 3
K là giao điểm của AN và CD => K ( 0; -3 )
K là trung điểm AN => N ( -2; -5 )
=> Đường thẳng BC qua điểm M và N
\(\overrightarrow{MN}\left(-2;-8\right)\)=> VTPT của BC là: \(\overrightarrow{n}\left(8;-2\right)\)
=> Phương trình BC : \(8\left(x-0\right)+\left(-2\right)\left(y-3\right)=0\)
<=> 4x -y + 3 = 0
Vậy: BC : 4x - y + 3 = 0
29 tháng 4 2020
Hướng dẫn:
Qua đường phân giác trong góc B lấy điểm B' đối xứng với A => B' thuộc BC và tìm được tọa độ B'
Qua đường phân giác trong góc C lấy điểm C' đối xứng với A => C' thuộc BC và tìm được tọa độ C'
=> Phương trình BC đi qua B' và C' .
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 3 2021
Tọa độ B là nghiệm: \(\left\{{}\begin{matrix}4x-y+3=0\\x-2y+1=0\end{matrix}\right.\) \(\Rightarrow B\left(-\dfrac{5}{7};\dfrac{1}{7}\right)\)
Tọa độ C là nghiệm: \(\left\{{}\begin{matrix}4x-y+3=0\\x+y+3=0\end{matrix}\right.\) \(\Rightarrow C\left(-\dfrac{6}{5};-\dfrac{9}{5}\right)\)
Phương trình đường thẳng qua C và vuông góc phân giác góc B:
\(2\left(x+\dfrac{6}{5}\right)+1\left(y+\dfrac{9}{5}\right)=0\Leftrightarrow2x+y+\dfrac{21}{5}=0\)
Gọi E là hình chiếu của C lên phân giác góc B \(\Rightarrow\left\{{}\begin{matrix}2x+y+\dfrac{21}{5}=0\\x-2y+1=0\end{matrix}\right.\) \(\Rightarrow E\left(-\dfrac{47}{25};-\dfrac{11}{25}\right)\)
Gọi F là điểm đối xứng E qua phân giác góc B \(\Rightarrow\) F thuộc AB đồng thời E là trung điểm CF \(\Rightarrow F\left(-\dfrac{64}{25};\dfrac{23}{25}\right)\)
\(\Rightarrow\overrightarrow{BF}\Rightarrow\) pt BF (chính là phương trình AB)
Làm tương tự với AC
CM
13 tháng 4 2019
Đáp án B
Do AB và BC cắt nhau tại B nên toa độ điểm B là nghiệm hệ phương trình
Do đó: B( 2; -1)
Tương tự: tọa độ điểm C( 1; 9)
PT các đường phân giác góc A là:
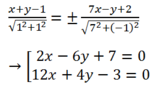
Đặt T1(x; y) = 2x- 6y+ 7 và T2= 12x+ 4y-3 ta có:
T1(B). T1(C) < 0 và T2(B) T2(C) >0.
Suy ra B và C nằm khác phía so với đường thẳng 2x-6y+7= 0 và cùng phía so với đường thẳng: 12x+ 4y- 3= 0.
Vậy phương trình đường phân giác trong góc A là: 2x- 6y+ 7= 0.
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 4 2021
1.
\(\overrightarrow{OA}=\left(1;3\right)\Rightarrow OA=\sqrt{10}\)
Gọi I là trung điểm OA \(\Rightarrow I\left(\dfrac{1}{2};\dfrac{3}{2}\right)\)
Phương trình đường tròn đường kính OA nhận I là trung điểm và có bán kính \(R=\dfrac{OA}{2}=\dfrac{\sqrt{10}}{2}\):
\(\left(x-\dfrac{1}{2}\right)^2+\left(y-\dfrac{3}{2}\right)^2=\dfrac{5}{2}\)
b.
Gọi 2 trung tuyến là BN và CM (với M, N là trung điểm AB và AC)
B thuộc BN nên tọa độ có dạng: \(\left(b;1\right)\)
M là trung điểm AB \(\Rightarrow M\left(\dfrac{b+1}{2};2\right)\)
M thuộc CM nên tọa độ thỏa mãn:
\(\dfrac{b+1}{2}-4+1=0\Rightarrow b=5\Rightarrow B\left(5;1\right)\)
\(\Rightarrow\overrightarrow{AB}=\left(4;-2\right)\Rightarrow\) pt AB: \(\left\{{}\begin{matrix}x=1+2t\\y=3-t\end{matrix}\right.\)
Gọi G là trọng tâm tam giác ABC \(\Rightarrow\) G là giao điểm BN và CM
Tọa độ G thỏa mãn: \(\left\{{}\begin{matrix}y-1=0\\x-2y+1=0\end{matrix}\right.\) \(\Rightarrow G\left(1;1\right)\)
\(\Rightarrow\left\{{}\begin{matrix}x_C=3x_G-x_A-x_B=-3\\y_C=3y_G-y_A-y_B=-1\end{matrix}\right.\) \(\Rightarrow C\left(-3;-1\right)\)
Biết tọa độ C, A, B bạn tự viết pt 2 cạnh còn lại
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 4 2021
2.
AB vuông góc với trung trực của AB nên nhận (2;-3) là 1 vtpt và (3;2) là 1 vtcp
Phương trình tham số:
\(\left\{{}\begin{matrix}x=-1+3t\\y=-3+2t\end{matrix}\right.\)
Phương trình tổng quát:
\(2\left(x+1\right)-3\left(y+3\right)=0\Leftrightarrow2x-3y-7=0\)
b. Câu này tìm trung điểm của AB hay BC nhỉ? Ta chỉ có thể tìm được trung điểm BC sau khi hoàn thành câu c (nghĩa là thứ tự bài toán bị ngược)
Gọi N là trung điểm AB \(\Rightarrow\) tọa độ N thỏa mãn:
\(\left\{{}\begin{matrix}2x-3y-7=0\\3x+2y-4=0\end{matrix}\right.\) \(\Rightarrow N\left(2;-1\right)\)
N là trung điểm AB \(\Rightarrow\left\{{}\begin{matrix}x_B=2x_N-x_A=5\\y_B=2y_N-y_A=1\end{matrix}\right.\) \(\Rightarrow B\left(5;1\right)\)
G là trọng tâm tam giác nên: \(\left\{{}\begin{matrix}x_C=3x_G-x_A-x_B=8\\y_C=3y_G-y_A-y_B=-4\end{matrix}\right.\) \(\Rightarrow C\left(8;-4\right)\)
\(\Rightarrow M\left(\dfrac{13}{2};-\dfrac{3}{2}\right)\)