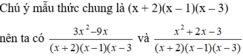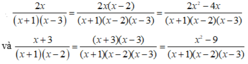Biến đổi phân thức x^2-7/4x+3 với x khác -3/4 và x khác 0 thành 1 phần thức bằng nó và có mẫu thức B=12x^2+9x
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
13 tháng 6 2016
a) \(\frac{4x+3}{x^2-5}=\frac{\left(4x+3\right).3x}{\left(x^2-5\right).3x}=\frac{12x^2+9x}{3x\left(x^2-5\right)}\)
b) \(\frac{8x^2-8x+2}{\left(4x-2\right)\left(15x-1\right)}=\frac{2\left(4x^2-4x+1\right)}{2\left(2x-1\right)\left(15x-1\right)}=\frac{\left(2x-1\right)^2}{\left(2x-1\right)\left(15x-1\right)}=\frac{2x-1}{15x-1}\)
11 tháng 9 2019
a ) \(\frac{4x+3}{x^2-5},A=12x2+9x\)
Suy ra \(\frac{4x+3}{x^2-5}=\frac{\left(4x+3\right).3x}{\left(x^2-5\right).3x}=\frac{12x^2+9x}{3x^3-15x}\)
Chúc bạn học tốt !!!
H9
HT.Phong (9A5)
CTVHS
24 tháng 7 2023
Ta có:
\(\dfrac{x^2-4}{x+1}\)
\(=\dfrac{\left(x+2\right)\left(x-2\right)}{x+1}\)
Và:
\(\dfrac{x+2}{2x}\)
\(=\dfrac{\left(x+2\right)\left(x-2\right)}{2x\left(x-2\right)}\)
Vậy ta đã biến đổi hai phân thức đó để chúng bằng phân thức cũ và có tủ bằng nhau