Cho hình trụ có bán kính đáy bằng 3 và thể tích bằng 18 π . Tính diện tích xung quanh S x q của hình trụ
A. S x q = 18 π
B. S x q = 36 π
C. S x q = 12 π
D. S x q = 6 π
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

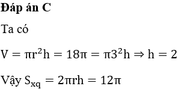

1:
V=pi*r^2*h
=>r^2*15*pi=375pi
=>r^2=25
=>r=5
Sxq=2*pi*r*h=2*5*15*pi=150pi

Đường cao: 3 x 2 = 6(cm)
a, Diện tích xung quanh hình trụ:
\(S_{xq}=2\pi rh=2.\pi.3.6=36\pi\left(cm^2\right)\)
b, Diện tích toàn phần hình trụ:
\(S_{tp}=2.S_{đáy}+S_{xq}=2.\pi r^2+36\pi=2\pi.3^2+36\pi=54\pi\left(cm^2\right)\)
c, Thể tích hình trụ:
\(V=\pi r^2.h=\pi.3^2.6=54\pi\left(cm^3\right)\)

Đáp án A
Gọi chiều cao của hình trụ là h
Ta có:
S x q = 2 π R 2 h ⇔ 2 π . 5 2 . h = 300 π ⇒ h = 6 ( c m )

Chọn A.
Hình trụ có bán kính đáy a và đường cao a 3 nên:
S xq = 2 π rh = 2 π a.a 3 = 2 π a 2 3

Chọn A.
Gọi r là bán kính đáy của hình trụ, h là chiều cao của hình trụ.
Theo bài ra ta có:
S = 2 π r h π r 2 = 4 π a 2 ⇔ r = 2 a h = S 4 π a
Thể tích khối trụ là:
V = π r 2 h = π 4 a 2 · S 4 π a = S a