Cho tam giác ABC có diện tích 75 cm vuông. Trên BC lấy M sao cho BM = 2/3 BC. Tính diện tích tam giác ABM.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Nhận xét : Ta thấy tam giác ABM và tam giác ABC có cùng chiều cao là AH ; hai đáy tương ứng là BM và BC. Do đó đáy và diện tích là hai đại lượng tỉ lệ thuận với nhau.
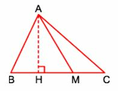
ở đây tỉ số về hai đáy là : BM/BC = 2/3. Vậy tỉ số về diện tích của hai tam giácABM và ABC là 2/3. Vì diện tích tam giác ABC bằng 75 c m 2 , nên diện tích tam giác ABM là :
75 : 3 x 2 = 50 ( c m 2 ).
Đáp số : 50 c m 2

ọi AH là đg cao của tam giác ABC => AH cũng là đg cao của ABM, AMC (do M thuộc BC)
Do BM = 1/3MC => BM = 1/4BC và MC = 3/4BC
Ta có:
SABC = BC.AH : 2 = 23,4
SABM = BM.AH : 2 = 1/4.BC.AH : 2 = 1/4.23,4 = 5,85
SAMC = SABC - SABM = 23,4 - 5,85 = 17,55

Vì BE=1313× BC mà ABE và ABC chung chiều cao hạ từ A
nên SABESABE=1313 ×=217,5 : 3 = 72,5(cm2)
⇒SADESADE+SBDESBDE=SABESABE \
⇒SADESADE= SABESABE-SBEDSBED
⇒SADESADE =72,5 – 14,55 = 57,95(cm2)
⇒ ADE và ABE chung chiều cao hạ từ E nên SADESABESADESABE=ADABADAB
⇒AB =SADESABESADESABE×AD=72,557,9572,557,95×8=10 (cm)
Cho tam giác ABC có diện tích 240 cm2. Trên BC lấy điểm D sao cho BD=3DC. Tínhdiện tích tam giác ABD. (ĐS cm2) là bài 3. Cho tam giác ABC có diện tích là 400 cm2. Điểm M trên AC sao cho 2xAM=3xCM.Tính diện tích tam giác ABM. (ĐS: cm2) là bài 4. Cho tam giác ABC có diện tích 720 cm2. Trên BC lấy M sao cho BM=1/2 CM. NốiAM , trên AM lấy N sao cho AN=3NM. Tính diện tích tam giác ABN. (ĐS: cm2) là bài 5 nhá các bạn. mình quên cách ra

Diện tích tam giác ABM là:
4.3=12(cm2)
Diện tích tam giác ABC là:
4.6=24(cm2)

Kẻ đường cao AH
\(\Rightarrow S_{ABM}=\dfrac{1}{2}BM\cdot AH=2AH=45\\ \Rightarrow AH=22,5\left(cm\right)\\ \Rightarrow S_{ABC}=\dfrac{1}{2}AH\cdot BC=\dfrac{1}{2}\cdot12\cdot22,5=135\left(cm^2\right)\)

\(\dfrac{S_{ABC}}{S_{ABM}}=\dfrac{BC}{BM}=\dfrac{12}{4}=3\\ \Rightarrow S_{ABM}=\dfrac{1}{3}S_{ABC}=15\left(cm^2\right)\)