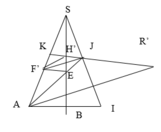
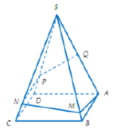
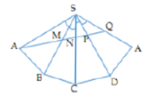
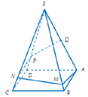
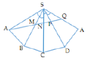
Thị xã Từ Sơn xây dựng một ngọn tháp đèn lộng lẫy hình chóp tứ giác đều S.ABCD có cạnh bên SA=12 m và ASB= 30 ° Người ta cần mặc một đường dây điện từ điểm A đến trung điểm K của SA gồm 4 đoạn thẳng AE, EF, FH, HK như hình vẽ. Để tiết kiệm chi phí ngừơi ta cần thiết kế được chiều dài con đường từ A đến K là ngắn nhất. Tính tỉ số K = H F + H K E A + E F
A. k = 3 4
B. k = 1 2
C. k = 1 3
D. k = 2 3

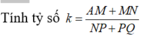
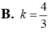
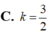
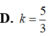



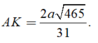
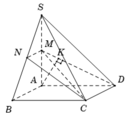
Đáp án B
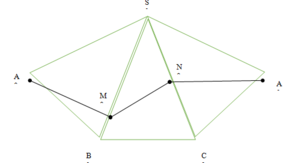
Gọi F’,H’ là điểm đối xứng của F,H qua SO
( O là tâm của đáy)
⇒ EF'=EF, FH=F'H'
Gọi I,J là điểm đối xứng của A,F’ qua SB
⇒ EF ' = EJ , F ' H ' = H ' J
A E + EF'+F'H'+H'K=AE+EJ + H ' J + H ' K ≥ AJ + K J
Gọi R là điểm đối xứng của A qua SI ⇒ AJ = J R
⇒ AJ + K J = J R + K J ≥ K R
Vậy để AE+EF’+F’H’+H’K nhỏ nhất bằng KR thì
H ' J + H ' K = K J A E + EJ = AJ = J R
k = H F + H K E A + EF = H ' F ' + H ' K E A + EF' = K J J R = S K S A = 1 2