Cho khối chóp S.ABCD có thể tích bằng a 3 . Mặt bên SAB là tam giác đều cạnh a và đáy ABCD là hình bình hành. Khoảng cách giữa SA và CD bằng:
A. 2 a 3 .
B. a 3 .
C. a 2 .
D. 2 3 a .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
S A ⊂ S A B , C D / / S A B ⇒ d S A , C D = d C D , S A B = d C , S A B V S A B C = 1 2 V S A B C D = a 3 2 = 1 3 d C , S A B . S S A B ⇒ 1 3 d 1 2 a 3 2 = d 3 a 2 12 = a 3 2 ⇒ d = 2 3 a

Đáp án D.
Ta có
C D / / A B , C D ⊂ S A B A B ⊂ S A B ⇒ C D / / S A B
⇒ d C D ; S A = d C D ; S A B = d C ; S A B
Từ giả thiết, ta có V S . A B C D = a 3 ⇒ V S . A B C = 1 2 C S . A B C D = a 3 2 và S Δ S A B = a 2 3 4
Lại có
V S . A B C = V C . S A B = 1 3 d C ; S A B . S Δ S A B ⇒ d C ; S A B = 3 V S . A B C V Δ S A B = 2 3 a
Vậy d S A ; C D = d C ; S A B = 2 3 a

Đáp án là D.
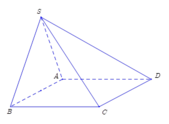
• Ta có:
C D / / A B A B ⊂ S A B ⇒ C D / / S A B ⇒ d S A ; C D = d C D ; S A B = d C ; S C D
• Gọi h = d C ; S A B ⇒ h = 3 V S . A B C S Δ S A B = 3 2 a 3 a 2 3 4 = 2 a 3
Đáp án D
S A ⊂ ( S A B ) , C D / / ( S A B ) ⇒ d ( S A , C D ) = d ( C D , ( S A B ) ) = d ( C , ( S A B ) ) V S A B C = 1 2 V S A B C D = a 3 2 = 1 3 d ( C , ( S A B ) ) . S S A B ⇒ 1 3 d 1 2 a 3 2 a = d 3 a 2 12 = a 3 2 ⇒ d = 2 3 a