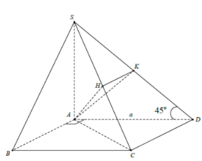
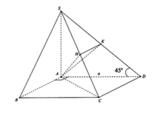
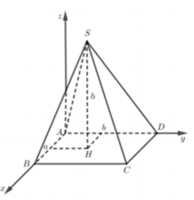
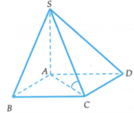
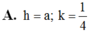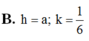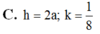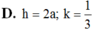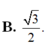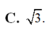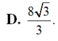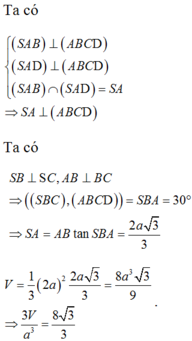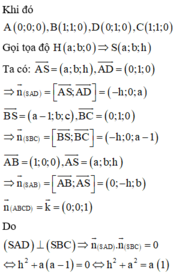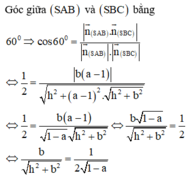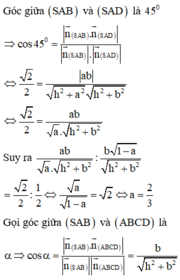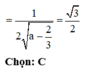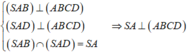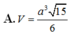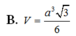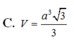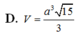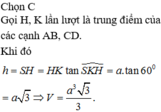Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Hai mặt bên (SAB) và (SAD) cùng vuông góc với mặt đáy. Biết góc giữa hai mặt phẳng (SCD) và (ABCD) bằng 45 ° . Gọi V 1 , V 2 lần lượt là thể tích khối chóp S.AHK và S.ACD với H, K lần lượt là trung điểm cùa SC và SD. Tính độ dài đường cao của khối chóp S.ABCD và tỉ số k= V 1 / V 2
A. h= a, k= 1/4
B. h= a, k= 1/6
C. h= 2a, k= 1/8
D. h= 2a, k= 1/3