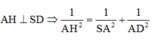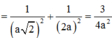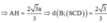Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, A B = a , B C = a 3 , S A = a và SA vuông góc với đáy ABCD. Tính sin α với α là góc tạo bởi đường thẳng BD và mặt phẳng (SBC)


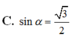

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


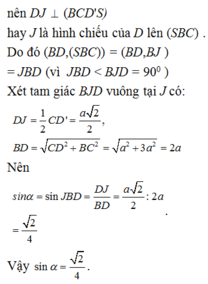

Chọn A
Phương pháp:
- Dựng hình hộp chữ nhật SB'C'D'.ABCD, xác định góc giữa BD và (SBC) (nhỏ hơn 90 0 ) là góc giữa
BD và hình chiếu của nó trên (SBC) .
- Sử dụng các kiến thức hình học đã học ở lớp dưới tìm sin α .
Cách giải:
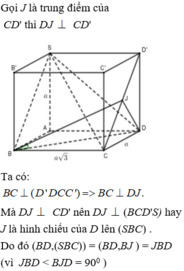
Qua B,C,D lần lượt kẻ các đường thẳng vuông góc với đáy.
Dựng hình hộp chữ nhật SB'C'D'.ABCD như hình vẽ.
Dễ thấy mặt phẳng (SBC) được mở rộng thành mặt phẳng (SBCD').
Tam giác D'DC có D'D = DC = a và D = 90 0 nên vuông cân tại D
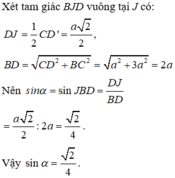

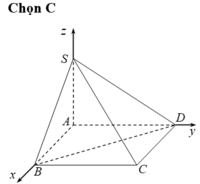
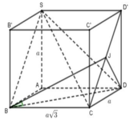
Đặt hệ trục tọa độ Oxyz như hình vẽ.
Khi đó, ta có A (0;0;0), B (a;0;0), D (0; a√3 ; 0), S (0;0;a).
Ta có ![]() , nên đường thẳng BD có vectơ chỉ phương là
, nên đường thẳng BD có vectơ chỉ phương là ![]() .
.
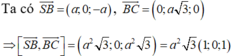
Như vậy, mặt phẳng (SBC) có vectơ pháp tuyến là ![]()
Do đó, α là góc tạo bởi giữa đường thẳng BD và mặt phẳng (SBC) thì
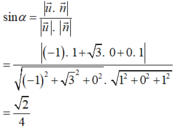

Chọn đáp án C.

ABCD là hình chữ nhật nên BD = 2a, ta có AD//(SBC) nên suy ra
![]()
với AH ⊥ SB. Tam giác SAB vuông cân tại A nên H là trung điểm của SB suy ra A H = a 2 2
Vậy
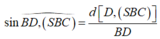
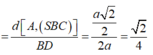

Chọn C
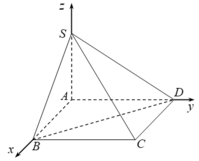
Đặt hệ trục tọa độ Oxyz như hình vẽ. Khi đó, ta có A (0; 0; 0), B (a; 0; 0), D (0; a√3; 0), S (0; 0; a)
Ta có ![]() , nên đường thẳng BD có vectơ chỉ phương là
, nên đường thẳng BD có vectơ chỉ phương là ![]()
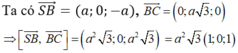
Như vậy, mặt phẳng (SBC) có vectơ pháp tuyến là ![]() . Do đó, α là góc tạo bởi giữa đường thẳng BD và mặt phẳng (SBC) thì:
. Do đó, α là góc tạo bởi giữa đường thẳng BD và mặt phẳng (SBC) thì:
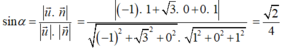

Đáp án C
Dựng hình bình hành SBCM. Kẻ D H ⊥ C M H ∈ C M
Ta có
B D ⊥ S B C = B D H ⊥ S B C ⇒ B D ; S B C ^ = B D ; B H ^ = D B H ^ = α
Tam giác CDM vuông cân tại D, có C D = a ⇒ D H = a 2 2
Tam giác BDH vuông tại H, có sin α = D H B D = 2 4 .
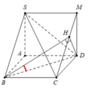

Đáp án A
Phương pháp: Cách xác định góc giữa đường thẳng và mặt phẳng:
Gọi a’ là hình chiếu vuông góc của a trên mặt phẳng (P).
Góc giữa đường thẳng a và mặt phẳng (P) là góc giữa đường thẳng a và a’.
Cách giải: ABCD là hình chữ nhật ![]()
![]()
Vì SA ⊥ (ABCD) nên (SC;(ABCD)) = (SC;AC) = S C A ^
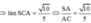
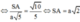
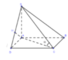
Ta có: AB//CD, CD ⊂ (SCD) => d(B;(SCD)) = d(A;(SCD))
Kẻ AH ⊥ SD, H ∈ SD
Ta có: 
![]()
Mà AH ⊥ SD => AH ⊥ (SCD) => d(A;(SCD)) = AH
Tam giác SAD vuông tại A,