Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và chiều cao bằng 2a. Diện tích xung quanh của hình nón đỉnh S và đáy là hình tròn nội tiếp hình vuông ABCD bằng
A. π a 2 17 4
B. π a 2 15 4
C. π a 2 15 2
D. π a 2 17 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Do ABCD là hình vuông nên hình tròn nội tiếp ABCD có bán kính là r = a 2
Vậy diện tích xung quanh của hình nón cần tìm là
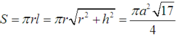

Đáp án A
Gọi O là tâm của hình vuông ABCD.
Do S.ABCD là hình chóp đều nên SO ⊥ (ACBD)
Suy ra, OB là hình chiếu vuông góc của SB lên mp(ABCD)


Đáp án C
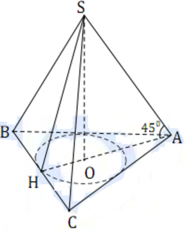
Gọi O là tâm đường tròn nội tiếp ∆ ABC.Theo giả thiết, góc giữa cạnh bên và đáy chính là góc giữa SA và OA hay S A O ^ = 45 o .Diện tích xung quanh cần tính là: S x q = π R l
Tam giác ABC đều cạnh 2a nên AH =a 3
Suy ra:
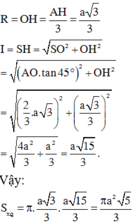

Đáp án C
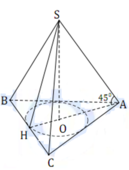
Gọi O là tâm đường tròn nội tiếp tam giác ABC.
Theo giả thiết, góc giữa cạnh bên và đáy chính là góc giữa SA và OA hay SAO ⏜ = 45 ° .
Diện tích xung quanh cần tính là: S xq = πRl
Tam giác ABC đều cạnh 2a nên AH = a 3
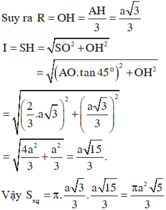
Đáp án A