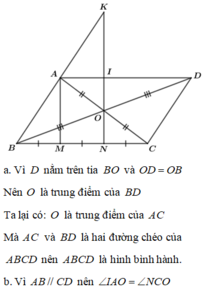
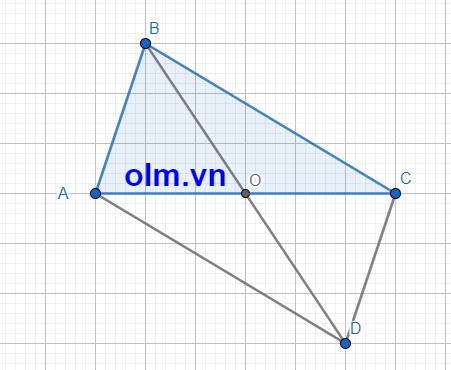
Cho tam giác ABC có O là trung điểm của cạnh AC. Trên tia BO lấy điểm D sao cho OD=OB.
a. Chứng minh tứ giác ABCD là hình bình hành.
b. Trên cạnh BC lấy điểm M,N sao cho BM=MN=NC. Tia NO cắt AD,AB lần lượt tại I và K. Chứng minh AI=NC và AM song song với IN.