Trong một lớp có (2n +3) học sinh gồm An, Bình, Chi cùng 2n học sinh khác. Khi xếp tùy ý các học sinh này vào dãy ghế được đánh số từ 1 đến (2n +3), mỗi học sinh ngồi một ghế thì xác xuất để số ghế của An, Bình, Chi theo thứ tự lập thành cấp số cộng là 17 1155 . Số học sinh của lớp là:
A. 27.
B. 25.
C. 45.
D. 35.




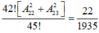
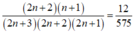

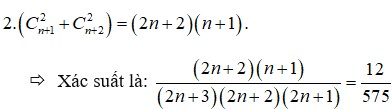




Đáp án là D