Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B , S A ⊥ A B C và AHlà đường cao của tam giác SAB Khẳng định nào sau đây sai
A. S B ⊥ B C
B. A H ⊥ B C
C. S B ⊥ A C
D. A H ⊥ S C
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
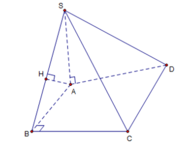
Ta có B C ⊥ S A B C ⊥ A B ⇒ B C ⊥ S A B ⇒ A H ⊥ B C
LẠI CÓ A H ⊥ S B ⇒ A H ⊥ S B C
Các ý A, C, D đúng

A là khẳng định sai.
Vì \(SB\perp\left(ABC\right)\) nên \(SB\perp BC\)
Nếu \(SA\perp BC\Rightarrow SA||SB\) hoặc SA trùng SB (đều vô lý)

Chọn B.
+) Vì tam giác ABC vuông tại B nên BC ⊥ AB.
- Lại có:
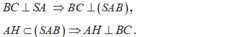
+) Theo gt AH ⊥ SB vậy:
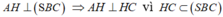
- Do đó AH không thể vuông góc với AC.(Một tam giác không thể có đồng thời hai góc vuông)
Đáp án C
Tam giác ABC vuông tại B ⇒ A B ⊥ B C
Mà S A ⊥ A B C ⇒ S A ⊥ B C ⇒ B C ⊥ S A B ⇒ B C ⊥ S B
Và A H ⊥ B C mà A H ⊥ S B ⇒ A H ⊥ S B C ⇒ A H ⊥ B C A H ⊥ S C
Vậy hai đường thẳng S B , A C chéo nhau.