
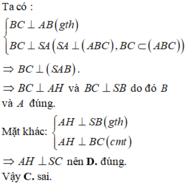
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


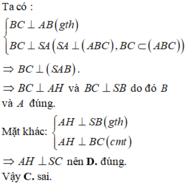

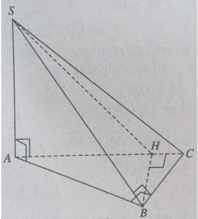
Kẻ \(BK\perp AC\Rightarrow BK\perp\left(SAC\right)\)
\(\Rightarrow BK=d\left(B;\left(SAC\right)\right)\)
\(\dfrac{1}{BK^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\Rightarrow BK=\dfrac{AB.AC}{\sqrt{AB^2+AC^2}}=\dfrac{a\sqrt{3}}{2}\)
Kẻ \(CP\perp BH\Rightarrow CP\perp\left(SBH\right)\)
\(\Rightarrow CP=d\left(C;\left(SBH\right)\right)\)
\(\widehat{CBP}=\widehat{ACB}=30^0\Rightarrow CH=BC.sin30^0=\dfrac{a\sqrt{3}}{2}\)
\(BH=\dfrac{AC}{2}=\dfrac{1}{2}\sqrt{AB^2+AC^2}=a\)\(\Rightarrow SH=\sqrt{SB^2-BH^2}=a\)
Kẻ \(HE\perp BC\) , kẻ \(HF\perp SE\Rightarrow HF=d\left(H;\left(SBC\right)\right)\)
\(HE=CH.sin30^0=\dfrac{a}{2}\)
\(\dfrac{1}{HF^2}=\dfrac{1}{SH^2}+\dfrac{1}{HE^2}\Rightarrow HF=\dfrac{SH.HE}{\sqrt{SH^2+HE^2}}=\dfrac{a\sqrt{5}}{5}\)

A là khẳng định sai.
Vì \(SB\perp\left(ABC\right)\) nên \(SB\perp BC\)
Nếu \(SA\perp BC\Rightarrow SA||SB\) hoặc SA trùng SB (đều vô lý)

a) BC ⊥ SA & BC ⊥ AB) ⇒ BC ⊥ (SAB)
⇒ BC ⊥ SB.
⇒ tam giác SBC vuông tại B.
b) BH ⊥ AC & BH ⊥ SA ⇒ BC ⊥ (SAC)
⇒ (SBH) ⊥ (SAC).
c) d[B, (SAC)] = BH. Ta có:
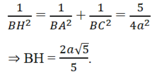

Chọn A

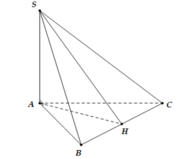
Gọi H là trung điểm của AC. Đỉnh S cách đều các điểm A, B, C
=> SH ⊥ (ABC)
Xác đinh được
![]()
Ta có MH // SA
![]()
Gọi I là trung điểm của AB => HI ⊥ AB
![]()
và chứng minh được HK ⊥ (SAB)
![]()
Trong tam giác vuông SHI tính được
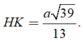

Chọn D.
+) Ta có :
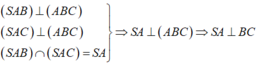
⇒ Suy ra : A đúng.
+) Ta có : 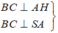
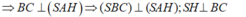
⇒ Suy ra : C đúng.
+) Mặt khác : AH ⊥ CD nên:
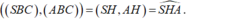
⇒ Suy ra : D sai.