Cho cấp số cộng u n có u 5 = - 15 , u 20 = 60 . Tổng S 20 của 20 số hạng đầu tiên của cấp số cộng là
A. S 20 = 600
B. S 20 = 60
C. S 20 = 250
D. S 20 = 500
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Gọi u1,du1,d lần lượt là số hạng đầu và công sai của cấp số cộng
Ta có: {u5=−15u20=60u5=-15u20=60.
Vậy S10=102.(2u1+9d)=−125
\(\left\{{}\begin{matrix}u_5=-15\\u_{20}=60\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}u_1+4d=-15\\u_1+19d=60\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}u_1=-35\\d=5\end{matrix}\right.\)
\(\Rightarrow S_{20}=\dfrac{20.\left(u_1+u_{20}\right)}{2}\)
\(=10\left(2u_1+19d\right)\)
\(=10\left(-2.35+19.5\right)\)
\(=250\)

Đáp án C.
Gọi số hạng đầu và công sai của CSC (un) là u1, d ta có
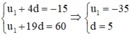
Suy ra ![]()

Phương pháp:
S n = n u 1 + n ( n - 1 ) d 2
Cách giải:
Ta có:
![]()
⇒ S 20 = n u 1 + n ( n - 1 ) 2 d = - 320
Chọn C

\(\left\{{}\begin{matrix}u_1+d=3\\u_1+9d=-15\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}u_1=\dfrac{21}{4}\\d=-\dfrac{9}{4}\end{matrix}\right.\)
\(S_{20}=\dfrac{21}{4}.20+\dfrac{19.20}{2}.\left(-\dfrac{9}{4}\right)=-\dfrac{645}{2}\)

Theo đề, ta có: \(S_n=3003\)
=>\(n\cdot\dfrac{\left[2u1+\left(n-1\right)\cdot d\right]}{2}=3003\)
=>\(\dfrac{n\left[2+\left(n-1\right)\right]}{2}=3003\)
=>n(n+1)=6006
=>n^2+n-6006=0
=>(n-77)(n+78)=0
=>n=77(nhận) hoặc n=-78(loại)
Vậy: n=77