Chứng tỏ tổng số đo các góc ngoài ở ba đỉnh của một tam giác bằng 3600.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
24 tháng 11 2021
a. B = 55 độ
C = 35
b. lỗi. phải là 360 độ
ông họ ngô
tôi họ đinh
PT
1
CM
30 tháng 8 2017
Tổng số đo của góc trong và góc ngoài ở mỗi đỉnh của hình n-giác bằng 180 0 . Hình n-giác có n đỉnh nên tổng số đo các góc trong và góc ngoài của đa giác bằng n. 180 0 . Mặt khác, ta biết tổng các góc trong của hình n-giác bằng (n – 2). 180 0
Vậy tổng số đo các góc ngoài của hình n-giác là:
n. 180 0 – (n – 2). 180 0 = n. 180 0 – n. 180 0 + 2. 180 0 = 360 0
CT
1
NM
0
N
2
6 tháng 1 2016
3600, tớ nhớ câu này tớ làm r nek , bấm vào câu hỏi tươg tự xem thử coi có k
PT
1
CM
26 tháng 7 2018
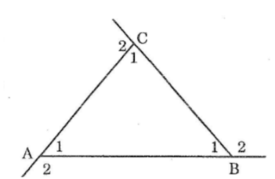
Ta có: ∠(A1 ) +∠(A2 ) =180o(hai góc kề bù)
∠(B1 ) +∠(B2 ) =180o(hai góc kề bù)
∠(C1 ) +∠(C2 )=180o(hai góc kề bù)
Suy ra: ∠(A1 ) +∠(A2 ) +∠(B1) +∠(B2 ) +∠(C1 ) +∠(C2 ) = 180º + 180º + 180º =540o
⇒∠(A2 ) + ∠( B2 ) +∠(C2 ) =540o-(∠(A1 ) +∠(B1 ) +∠(C1 ) ) (1)
Trong ΔABC, ta có:
∠(A1 ) +∠(B1 ) +∠(C1 ) =180o (tổng ba góc trong tam giác) (2)
Từ (1) và (2) suy ra: ∠(A2 ) +∠(B2 ) +∠(C2 ) =540o-180o=360o
NP
2
10 tháng 1 2016
Mỗi góc ngoài của một tam giác bằng tổng của hai góc trong không kề với nó.
LA
9 tháng 7 2017
Tam giác ABC có: góc B +góc C + góc BAC = 180 o => 40 o + 40 o + BAC = 180 o => góc BAC = 180 o - 80 o = 100 o
=> góc BAy = 180 o - BAC = 180 o - 100 o = 80 o (do BAy là góc ngoài tam giác )
=> góc xAB = yAB/2 = 80 o/2 = 40 o (do Ax là p/g của góc yAB)
=> góc xAB = ABC (= 40 o) Mà hai góc này ở vị trí SLT => Ax // BC
Lời giải:
Gọi $\widehat{A}, \widehat{B}, \widehat{C}$ là 3 góc trong tam giác $ABC$ và $\widehat{A_1}, \widehat{B_1}, \widehat{C_1}$ tương ứng là 3 góc ngoài 3 đỉnh.
Ta có:
$\widehat{A_1}+\widehat{B_1}+\widehat{C_1}=(180^0-\widehat{A})+(180^0-\widehat{B})+(180^0-\widehat{C})$
$=540^0-(\widehat{A}+\widehat{B}+\widehat{C})$
$=540^0-180^0=360^0$