Một con lắc lò xo thẳng đứng gồm lò xo nhẹ có độ cứng k = 25 N/m một đầu được gắn với hòn bi nhỏ có khối lượng m = 100 g. Khi vật đang ở vị trí cân bằng, tại thời điểm t = 0 người ta thả cho con lắc rơi tự do sao cho trục lò xo luôn nằm theo phương thẳng đứng và vật nặng ở phía dưới lò xo. Đến thời điểm t 1 = 0 , 02 15 s thì điểm chính giữa của lò xo đột ngột bị giữ lại cố định. Lấy g = 10 m / s 2 , π 2 = 10 . Bỏ qua ma sát, lực cản. Tốc độ của hòn bi tại thời điểm t 2 = t 1 + 0 , 07 s có độ lớn gần nhất với giá trị nào sau đây?
A. 45 cm/s
B. 60 cm/s
C. 90 cm/s
D. 120 cm/s




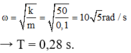
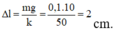
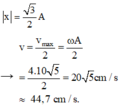


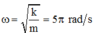
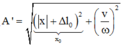
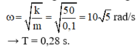

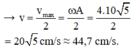


Chọn đáp án A
@ Lời giải:
Ban đầu lò xo giãn một đoạn Δ l 0 , sau khoảng thời gian thả rơi lò xo và vật → lò xo co về trạng thái không biến dạng. Khi ta giữ cố định điểm chính giữa của lò xo, con lắc sẽ dao động quanh vị trí cân bằng mới.
+ Khi giữ cố định điểm chính giữa của lò xo, phần lò xo tham gia vào dao động có độ cứng k = 2 k 0 = 50 N / m .
→ Tần số góc của dao động ω = k m = 50 0 , 1 = 10 5 rad/s → T = 0,28 s.
→ Độ biến dạng của lò xo tại vị trí cân bằng mới Δ l = m g k = 0 , 1.10 50 = 2 cm.
+ Vận tốc của con lắc tại thời điểm t 1 là v 0 = g t 1 = 10.0 , 02 15 = 0 , 2 15 m/s.
→ Biên độ dao động của con lắc A = Δ l 2 + v 0 ω 2 = 2 2 + 20 15 10 5 2 = 4 cm.
+ Ta chú ý rằng tại thời điểm t 1 vật ở vị trí có li độ x = A 2 = 2 cm → sau khoảng thời gian Δ t = t 2 – t 1 = 0 , 25 T = 0 , 07 s vật đi vị trí có li độ x = 3 2 A → v = v m a x 2 = ω A 2 = 4.10 5 2 = 20 5 cm/s ≈ 44,7 cm/s.