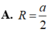
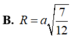
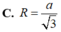
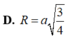
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án A
Phương pháp:
+ Xác định chiều cao của hình chóp
+ Xác định tâm và bán kính mặt cầu ngoại tiếp hình chóp:
Bước 1: Xác định tâm đường tròn ngoại tiếp hình vuông ABCD
Bước 2: Xác định trục đường tròn ngoại tiếp đa giác đáy. Kẻ đường trung trực một cạnh bên giao với trục đường tròn ở đâu đó chính là tâm mặt cầu ngoại tiếp hình chóp.
+ Tính bán kính mặt cầu ngoại tiếp hình chóp dựa vào định lý Pytago.
+ Mặt cầu có bán kính R thì có diện tích là S = 4 π R2
Cách giải:
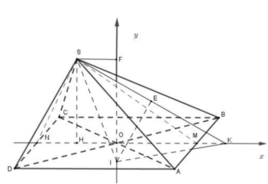
Chọn A.
Phương pháp:
+ Xác định chiều cao của hình chóp
+ Xác định tâm và bán kính mặt cầu ngoại tiếp hình chóp:
Bước 1: Xác định tâm đường tròn ngoại tiếp hình vuông ABCD
Bước 2: Xác định trục đường tròn ngoại tiếp đa giác đáy. Kẻ đường trung trực một cạnh bên giao với trục đường tròn ở đâu đó chính là tâm mặt cầu ngoại tiếp hình chóp.
+ Tính bán kính mặt cầu ngoại tiếp hình chóp dựa vào định lý Pytago.
+ Mặt cầu có bán kính R thì có diện tích là S = 4 π R 2
Cách giải:
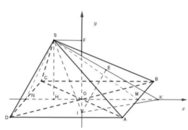
Gọi O là tâm hình vuông ABCD, gọi M , N lần lượt là trung điểm của AB; CD .
Kẻ SH ⊥ MN tại H .
Ta có SN ⊥ DC ; MN ⊥ DC
⇒ DC ⊥ ( SMN )
⇒ DC ⊥ SH
Mà SH ⊥ MN
⇒ SH ⊥ (ABCD).
Vì ABCD là hình vuông cạnh a nên:
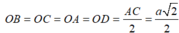
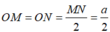
Vì tam giác SDC vuông cân tại S có cạnh huyền CD = a
⇒ SN= a 2
Vì tam giác ABS đều cạnh a
⇒ SM = a 3 2
Xét tam giác SNM có:
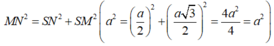
⇒ △ S M N vuông tại S.
Suy ra:
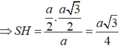
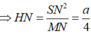
Nhận thấy O là tâm đường tròn ngoại tiếp hình vuông ABCD .
Kẻ tia Oy / /SH , khi đó tâm mặt cầu ngoại tiếp hình chóp S . ABCD nằm trên đường thẳng Oy.
Trên tia OM ta lấy K sao cho OK = OA = a 2 2 , khi đó K ∈ (O; OA)
Trong mặt phẳng (SMN ), lấy E là trung điểm SK , kẻ EI là đường trung trực của SK (I ∈ Oy).
Khi đó:
IK = IS = IA = IB = IC = ID nên I là tâm mặt cầu ngoại tiếp hình chóp S . ABCD và bán kính là R = IK.
Kẻ SF ⊥ Oy
Gắn hệ trục Oxy với OM ≡ Ox; Oy / /SH
Đặt I ( 0 , y o )
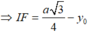
Xét tam giác vuông ISF có:
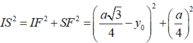
Xét tam giác vuông OIK có:
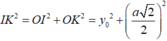
Vì 
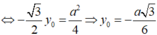
Suy ra bán kính mặt cầu:
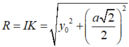
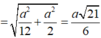
Diện tích mặt cầu ngoại tiếp hình chóp là:
Đáp án D
Gọi H là trung điểm của AB, do tam giác SAB đều nên SH ⊥ AB mà (SAB) ⊥ (ABCD) nên SH ⊥ (ABCD)
Gọi O là tâm của hình vuông ABCD, d là đường thẳng qua O và song song SH thì d ⊥ (ABCD) hay d là trục đường tròn ngoại tiếp hình vuông ABCD
Trong mặt phẳng (SAB) từ G kẻ đường thẳng vuông góc với (SAB) cắt d tại I thì I là tâm mặt cầu ngoại tiếp hình chóp S.ABCD, bán kính R = IS.
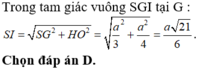
Đáp án B.
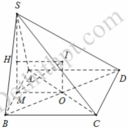
Gọi O là tâm của hính vuông ABCD và H là tâm của đường tròn ngoại tiếp Δ S A B . Từ O kẻ đường thẳng d vuông góc với (ABCD). Từ H kẻ đường thẳng H vuông góc với (SAB).
Ta có d ∩ Δ = I ⇒ I A = I B = I C = IS ⇒ I là tâm đường tròn ngoại tiếp khối chóp S . A B C D ⇒ R = I A = O I 2 + O A 2 .
Mà O I = H M = H B 2 − M B 2 với M là trung điểm của AB.
Xét Δ S A B cân tại S, có A B sin A S B ^ = 2 r
⇒ H B = r = 2 a 2. sin 120 0 = 2 a 3 .
Khi đó O I = 2 a 3 2 − a 2 = a 3 ⇒ R = a 3 2 + a 2 2 = a 21 3 .
Đáp án D.
Gọi H là trung điểm của AB thì S H ⊥ A B C D ⇒ S H = a 2 .
Khoảng cách từ H đến BC, CD, DA đều là a 2 3 ⇒ S A B C D = 1 2 . a 2 3 . 9 a − a = 2 a 2 3 .
Vậy thể tích khối chóp S.ABCD là V S . A B C D = 1 3 S H . S A B C D = 1 3 . a 2 . 2 a 2 3 = a 3 3 9 .
Đáp án B