Khi tính nguyên hàm ∫ x - 3 x + 1 d x , bằng cách đặt u = x + 1 ta được nguyên hàm nào
A. ∫ 2 u 2 - 4 d u
B. ∫ u 2 - 4 d u
C. ∫ u 2 - 3 d u
D. ∫ 2 u u 2 - 4 d u
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

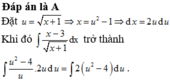

Ta có: \(\int\dfrac{xdx}{x^2+3}\)
Đặt \(u=x^2+3\left(u>0\right)\)
Có \(du=2xdx\)
\(\Rightarrow\int\dfrac{xdx}{x^2+3}=\)\(\int\dfrac{du}{2u}=\dfrac{1}{2}ln\left(u\right)=\dfrac{1}{2}ln\left(x^2+3\right)\)

Đáp án C
Với y = x 2 − 1 ⇒ d u = 2 x d x .
Vậy I = ∫ u d u .

Ý bạn là \(f(x)=\frac{1}{9+x^2}+\frac{3}{9+x^2}\) hay thế nào? Bạn cần viết đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo để được hỗ trợ tốt hơn).