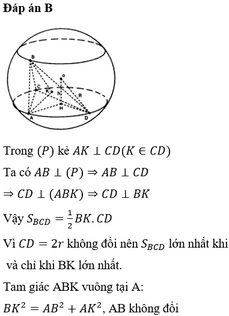
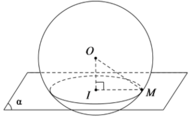
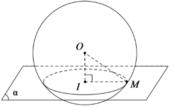
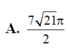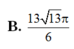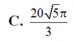Cho mặt cầu S(O;R) và (P) cách O một khoảng bằng h (0<h<R). Gọi (L) là đường tròn giao tuyến của mặt cầu (S) và (P) có bán kính r. Lấy A là một điểm cố định thuộc (L). Một góc vuông xAy trong (P) quay quanh điểm A. Các cạnh Ax, Ay cắt (L) ở C và D. Đường thẳng đi qua A và vuông góc với (P) cắt mặt cầu ở B. Diện tích ΔBCD lớn nhất bằng
A. 2 r r 2 + 4 h 2
B. r r 2 + 4 h 2
C. r r 2 + h 2
D. 2 r r 2 + h 2