Cho hình chóp S.ABCD có đáy là hình thang vuông tại A,B Biết S A ⊥ A B C D , A B = B C = a , A D = 2 a , S A = a 2 . Gọi E là trung điểm của AD. Tính bán kính mặt cầu đi qua các điểm S , A , B , C , E .
A. a 30 6
B. a 6 6
C. a 3 2
D. a
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
Gọi H là trung điểm của CD, M là trung điểm của BC. Khi đó HM ⊥ BC, SM ⊥ BC. Dễ thấy tam giác HBC vuông cân ở H, do đó tính được BC, SM. Từ đó tính được SH.

Đáp án D
Dựng HK ⊥ BD, do SH ⊥ BD nên ta có:
(SKH) ⊥ BD => Góc giữa hai mặt phẳng (SBD) và mặt phẳng đáy là góc SKH = 600
Lại có: ![]()
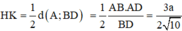
Do đó 
Vậy 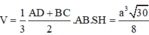

Chọn D
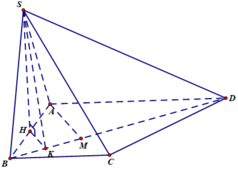
Ta có ![]()
Gọi H là trung điểm AB thì ![]() ,
,
kẻ ![]() , ta có
, ta có ![]() là góc giữa (SBD) và (ABCD), do đó
là góc giữa (SBD) và (ABCD), do đó ![]() = 600
= 600
Gọi AM là đường cao của tam giác vuông ABD. Khi đó, ta có:
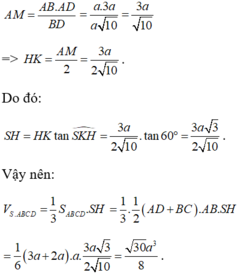
Đáp án D
Gọi I là trung điểm của SC. Khi đó I là tâm mặt cầu đi qua các điểm S, A, B, C, E
Ta có: A C = a 2 + a 2 = a 2 , S C = a 2 2 + a 2 2 = 2 a
bán kính mặt cầu đi qua các điểm S, A, B, C, E là: R = S C 2 = a