Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

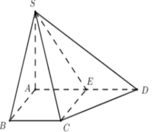
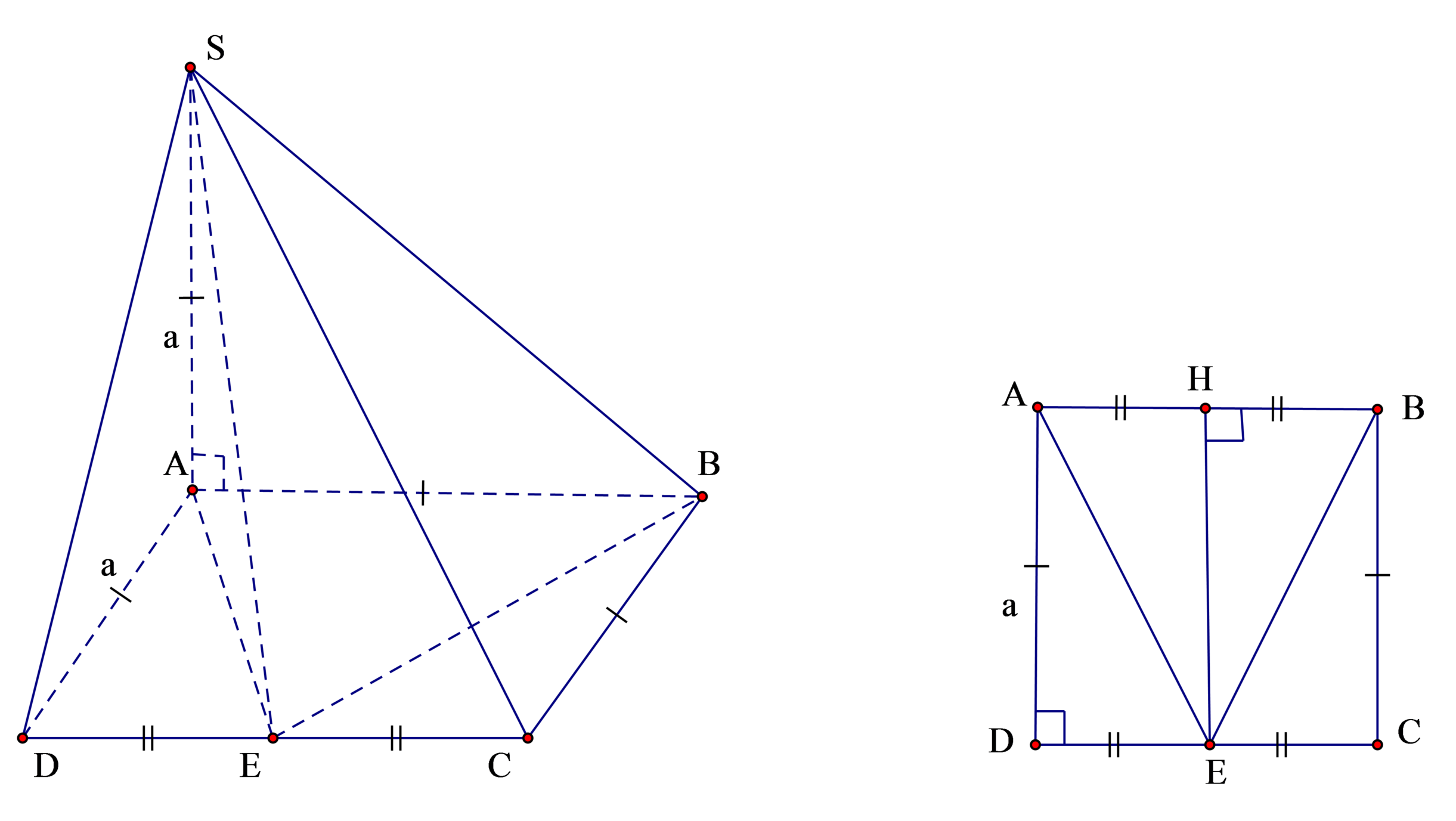
Xét tứ giác ABCE có
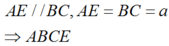
là hình bình hành.
Lại có
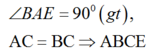
là hình vuông cạnh a.
Bán kính đường tròn ngoại tiếp hình vuông ABCE là
R d = a 2 2
Sử dụng công thức tính nhanh bán kính mặt cầu ngoại tiếp chóp
S.ABCE là:
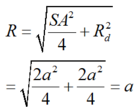
Chọn B.

Đáp án A
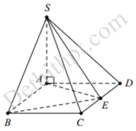
Hình chóp SABE có cạnh bên S A ⊥ đáy (ABE) ta có công thức tính bán kính mặt cầu của hình chóp dạng này là R = R d 2 + h 2 2 ( với R d là bán kính đường tròn ngoại tiếp đáy và h là chiều cao hình chóp )
Ta có: h = S A = a ; d t A B E = 1 2 E H . A B = a 2 2
A E = B E = a 2 + a 2 4 = a 5 2
R d = A B . A E . B E 4 d t A B E = a . 5 a 2 4 4. a 2 2 = a 5 8
vậy R = 25 a 64 2 + a 2 4 = a 41 8 .

Đáp án A
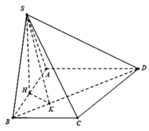
Tam giác ABE cân có A E = B E = a 5 2
và AB = a
⇒ S Δ A B E = a 2 2 = A E . B E . A B 4. R Δ A B E ⇒ R Δ A B E = 2 a . a 5 2 2 : 4 a 2 = 5 a 8
Vậy bán kính mặt cầu ngoại tiếp khối chóp S.ABE là
R = R Δ A B E 2 + S A 2 4 = 5 a 8 2 + a 2 4 = a 41 8

Đáp án D
Dựng HK ⊥ BD, do SH ⊥ BD nên ta có:
(SKH) ⊥ BD => Góc giữa hai mặt phẳng (SBD) và mặt phẳng đáy là góc SKH = 600
Lại có: ![]()
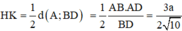
Do đó 
Vậy 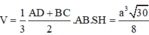

Đáp ván A
Vì I là hình chiếu của S trên (ABCD)
⇒ ( S C → , ( A B C D ) ) = S C I ⏞
⇒ S I = I C . tan 60 ° = a 5 2 . tan 60 ° = a 15 2
Vậy
V S . I B C = V S . A B C D - V S . A I B - V S . I C D = 1 3 . a 15 2 a + 2 a 2 . a - 1 2 . a 2 . 2 a - 1 2 . a 2 . a = a 3 15 8









Đáp án D
Gọi I là trung điểm của SC. Khi đó I là tâm mặt cầu đi qua các điểm S, A, B, C, E
Ta có: A C = a 2 + a 2 = a 2 , S C = a 2 2 + a 2 2 = 2 a
bán kính mặt cầu đi qua các điểm S, A, B, C, E là: R = S C 2 = a