Cho hàm số y = x 4 − 3 x 2 − 2. Tìm số thực dương m để đường thẳng y = m cắt đồ thị hàm số tại 2 điểm phân biệt A, B sao cho tam giác OAB vuông tại O, trong đó O là gốc tọa độ.
A. m = 2
B. m = 3 2
C. m = 3
D. m = 1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D
Phương trình hoành độ giao điểm :
![]()
Theo yêu cầu bài toán : ![]() phải có hai nghiệm phân biệt khác
phải có hai nghiệm phân biệt khác ![]()
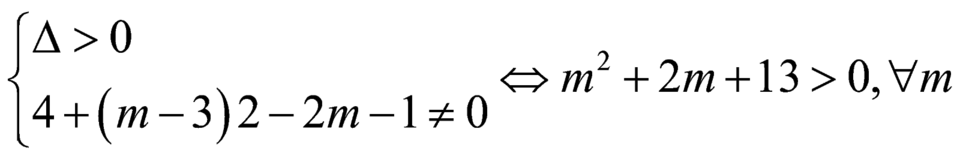
Gọi ![]() ,
,![]() suy ra
suy ra ![]() là trọng tâm của tam giác
là trọng tâm của tam giác ![]() :
:
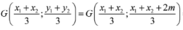
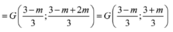
Theo yêu cầu bài toán :
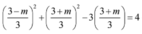
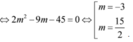 .
.

Đáp án D
PTHĐGĐ: x 2 + ( m − 3 ) x − 2 m − 1 = 0 ( * ) ĐK: ( m − 3 ) 2 + 4 ( 2 m + 1 ) > 0
Gọi x1, x2 là 2 nghiệm phân biệt của (*) ⇒ A x 1 ; x 1 + m , B x 2 ; x 2 + m với S = x1 + x2 = 3 – m
Gọi G là trọng tâm tam giác OAB ⇒ G x 1 + x 2 3 ; x 1 + x 2 + 2 m 3 ⇒ G S 3 ; S + 2 m 3
G ∈ ( C ) : x 2 + y 2 − 3 y = 4
⇒ S 9 2 + ( S + 2 m ) 9 2 − ( S + 2 m ) = 4 ⇔ S 2 + ( S + 2 m ) 2 − 9 ( S + 2 m ) = 36
⇔ ( 3 − m ) 2 + ( 3 + m ) 2 − 9 ( 3 + m ) = 36 ⇔ 2 m 2 − 9 m − 45 = 0 ⇔ m = − 3 ( n ) m = 15 2 ( n )

Đáp án C
Điều kiện: x≠2.
Hoành độ giao điểm của hai đồ thị là nghiệm của phương trình
2 x x − 2 = x + m ⇔ 2 x x − 2 − x − m = 0 ⇔ 2 x − x 2 + 2 x − m x + 2 m x − 4 = 0 ⇔ − x 2 + 4 − m x + 2 m x − 2 = 0.
Để hai đồ thị hàm số giao nhau tại hai điểm phân biệt A,B ta có
4 − m 2 + 8 m > 0 g 2 ≠ 0 ⇔ m 2 + 16 > 0 − 4 + 8 − 2 m + 2 m ≠ 0
thỏa mãn với mọi m ∈ ℝ .
Theo bài ra ta có x A + x B + x O = 3 x A + m + x B + m + y O = 7 ⇔ 4 − m = 3 4 − m + 2 m = 5 ⇔ m = 1 .
Vậy m=1 thỏa mãn điều kiện đề bài.

- Xét phương trình hoành độ giao điểm :\(x^2-2x+2=x+m\)
\(\Leftrightarrow x^2-3x+2-m=0\)
Có \(\Delta=b^2-4ac=9-4\left(2-m\right)=9-8+4m=4m+1\)
- Để (d) cắt (P) tại 2 điểm phân biệt thì \(\Delta>0\) \(\Leftrightarrow m>-\dfrac{1}{4}\left(1\right)\)
Theo viet : \(\left\{{}\begin{matrix}x_a+x_b=3\\x_ax_b=2-m\end{matrix}\right.\)
- Ta có : \(OA^2+OB^2=10\)
\(\Leftrightarrow x^2_A+y^2_A+x_B^2+y^2_B=10\)
\(\Leftrightarrow x^2_a+x^2_b+\left(x_a+m\right)^2+\left(x_b+m\right)^2=10\)
\(\Leftrightarrow2x^2_a+2x^2_b+2m\left(x_a+x_b\right)+2m^2=10\)
\(\Leftrightarrow2\left(x_a+x_b\right)^2-4x_ax_b+2m\left(x_a+x_b\right)+2m^2-10=0\)
\(\Leftrightarrow18-4\left(2-m\right)+6m+2m^2-10=0\)
\(\Leftrightarrow2m^2+10m=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m=0\\m=-5\end{matrix}\right.\)
- Kết hợp ĐK (1) => m = 0 ( TM )
Vậy ...
ĐAp án A
Phương trình hoành độ giao điểm là: x 4 − 3 x 2 − 2 − m = 0 1
Gọi A x ; m ; B − x ; m là tọa độ giao điểm
Khi đó Δ O A B vuông tại O khi O A ¯ . O B ¯ = − x 2 + m 2 = 0 ⇔ x = m
Khi đó m 4 − 3 m 2 − 2 − m = 0 ⇔ m = 2 (thỏa mãn).