Một chất điểm dao động điều hòa trên đoạn thẳng dài 20 cm. Ở vị trí mà li độ của chất điểm là 5 cm thì nó có tốc độ 5π√3 cm/s. Dao động của chất điểm có chu kì là
A. 1s
B. 2s
C. 0,2s
D. 1,5s
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



- Áp dụng biểu thức liên hệ giữa vận tốc, li độ, biên độ và tần số góc ta có:
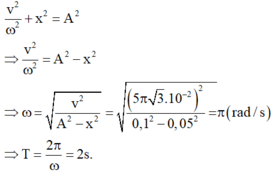

Đáp án B
Áp dụng biểu thức liên hệ giữa vận tốc, li độ, biên độ và tần số góc ta có
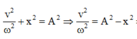
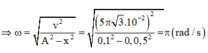
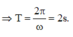

ü Đáp án C
+ Tần số góc của dao động
ω = v A 2 - x 2 = 0 , 5 rad/s
→ T = 4π s

+ Khi qua VTCB, vận tốc cực đại, nên: vmax=20 cm/s.
+ Do: \(a = v'_{(t)} \Rightarrow (v_{max})^2 = v^2+(\frac{a}{\omega})^2 \Rightarrow (20)^2 = 10^2+(\frac{40\sqrt 3}{\omega})^2 \Rightarrow \omega = 4\ (rad/s)\)
+ Biên độ: \(A = \frac{v_{max}}{\omega}=\frac{20}{4} = 5 \ (cm)\)

Đáp án D
+ Tốc độ của vật khi đi qua vị trí cân bằng v = v m a x = ω A = 20 c m / s
-> Gia tốc và vận tốc trong dao động điều hòa là vuông pha nhau, ta có công thức độc lập thời gian
v ω A 2 + a ω 2 A 2 = 1 ⇔ 10 20 2 + 40 3 20 ω 2 = 1 ⇒ ω = 4 r a d / s