Có bao nhiêu giá trị nguyên của m để đồ thị hàm số y = 6 x - 3 m x 2 - 6 x + 3 9 x 2 + 6 m x + 1 có đúng một đường tiệm cận
A. 1
B. 2
C. 0
D. Vô số
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




3.
\(y'=\dfrac{3m-1}{\left(x+3m\right)^2}\)
Hàm nghịch biến trên khoảng đã cho khi:
\(\left\{{}\begin{matrix}3m-1< 0\\-3m\le6\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m< \dfrac{1}{3}\\m\ge-2\end{matrix}\right.\)
\(\Rightarrow-2\le m< \dfrac{1}{3}\Rightarrow m=\left\{-2;-1;0\right\}\)
4.
\(y'=\dfrac{3m-2}{\left(x+3m\right)^2}\)
Hàm đồng biến trên khoảng đã cho khi:
\(\left\{{}\begin{matrix}3m-2>0\\-3m\ge-6\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m>\dfrac{2}{3}\\m\le2\end{matrix}\right.\)
\(\Rightarrow\dfrac{2}{3}< m\le2\Rightarrow m=\left\{1;2\right\}\)

Chọn đáp án A
Phương pháp
Nhẩm nghiệm của phương trình hoành độ giao điểm, từ đó tìm điều kiện để phương trình hoành độ giao điểm có 3 nghiệm phân biệt.

Để đồ thị hàm số cắt trục hoành tại ba điểm phân biệt thì phương trình x 2 + ( m + 3 ) x + m 2 = 0 phải có hai nghiệm phân biệt khác 1
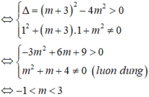
Do đó với -1<m<3 thì đồ thị hàm số cắt trục hoành tại 3 điểm phân biệt
![]()

Đáp án là A
Phương trình hoành độ giao điểm của đồ thị hàm số đã cho và trục hoành:
![]()
![]()
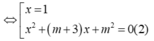
Đồ thị hàm số đã cho cắt trục hoành tại 3 điểm phân biệt ⇔ (1) có 3 nghiệm phân biệt ⇔ (2) có 2 nghiệm phân biệt khác 1
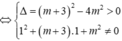
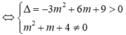
![]()
Do đó có 3 giá trị nguyên của m thỏa mãn ycbt.

Hàm số g(x) nghịch biến trên khoảng (0;1) khi ![]()
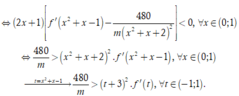
Dựa vào đồ thị, ta có
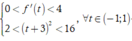
![]()
Theo YCBT 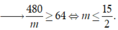
Chọn C.

TH1 : Đồ thị hàm số y = 3mx2 - (m - 9)x + 8 - m2 có hai điểm phân biệt đối xứng nhau qua gốc tọa độ khi hàm số trên là hàm số lẻ trên tập xác định R
Khi đó f(x) + f(-x) = 0
⇒ 3mx2 + 3mx2 - (m - 9)x + 8- m2 + (m - 9)x - m2 + 8 = 0
⇒ 6mx2 + 16 = 0 (không có m)